SilverSoldier
- 26
- 3
Suppose we add a weak acid HA into pure water, so that upon addition its initial concentration is c. The following equilibria should establish in the system. $$\text{HA}+\text{H}_2\text{O}\rightleftharpoons\text{H}_3\text{O}^++\text{A}^-$$ $$2\text{H}_2\text{O}\rightleftharpoons\text{H}_3\text{O}^++\text{OH}^−$$ Let ##K_a## and ##K_w## respectively be the equilibrium constants for these processes. We can express the composition of the system before and after equilibrium as follows. Let ##a## be the concentration of ##\text{H}_3\text{O}^+## and ##\text{OH}^−## already present in the system due to the autoionization of water initially; i.e., ##a=\sqrt{K_w}##.
Thus, we can obtain the following expressions at equilibrium. $$K_w=\left(a+p+q\right)\left(a+q\right)$$ $$K_a=\dfrac{\left(a+p+q\right)\left(p\right)}{c-p}$$ Taking ##r=a+q##, we obtain the following cubic equations in ##p## and ##r##. $$p^3K_a+p^2\left(K_a^2−K_w−cK_a\right)−2pcK_a^2+c^2K_a^2=0$$ $$r^3K_a+r^2\left(cK_a+K_w\right)−rK_aK_w−K_w^2=0$$ Now, as the acid begins to dissociate, because there is ##\text{H}_3\text{O}^+## already present in the system, the reverse "association" process should start off faster, so it should take lesser time for its rate to increase up to a significant value bringing the system to equilibrium, allowing time only for fewer molecules of the acid to dissociate.
At the same time, because ##\text{H}_3\text{O}^+## is being "removed" by the reverse autoionization process as it forms, the system should be trying to keep the ##\text{H}_3\text{O}^+## concentration below whatever value it would otherwise have risen to in the absence of autoionization.
The fact that the reverse autoionization process is triggered as the reaction proceeds should mean that ##\text{OH}^-## ions in the system should be being consumed, so by the time equilibrium is attained, its concentration must be lesser than the initial value. This means that ##r## in the equation above must be less than ##a##, so if ##a## can be considered small, then ##r^3## must be even smaller, and the effect of the ##r^3## term in the equation should be negligible. It should therefore be possible the reduce it to $$r^2\left(cK_a+K_w\right)−rK_aK_w−K_w^2=0$$ The following is a plot I made of the above equations with the ##x## axis representing ##c## and ##y## axis representing ##r##. The ##r^3## term is neglected in the orange curve, and not neglected in the black curve (##K_a=5## and ##K_w=0.5## here).
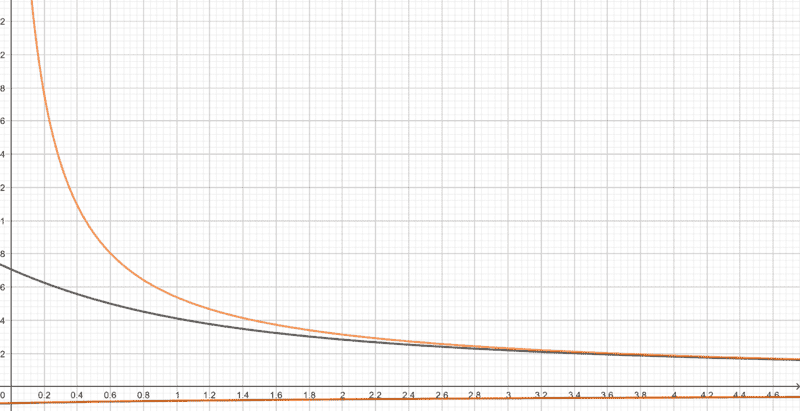
The orange curve greatly deviates from the black curve for small concentrations. Is this possible, because ##r## must always be less than ##a## for all concentrations? Have I made an error somewhere? Is it wrong to neglect the ##r^3## term?
By the way, I have not seen calculations being made taking the ##\text{H}_3\text{O}^+## and ##\text{OH}^-## concentrations already present in the system initially into consideration. Where the autoionization of water is not neglected it is always assumed that there are no ##\text{H}_3\text{O}^+## and ##\text{OH}^-## ions present in the system before equilibrium. Why is this? Is there anything wrong with saying it is already present?
##\text{HA}## | ##\text{H}_3\text{O}^+## | ##\text{A}^-## | |
| Initial concentration | ##c## | ##a## | - |
| Change in concentration | ##-p## | ##+p## | ##+p## |
| Equilibrium concentration | ##c-p## | ##a+p+q## | ##p## |
##\text{H}_2\text{O}## | ##\text{H}_3\text{O}^+## | ##\text{OH}^−## | |
| Initial concentration | - | ##a## | ##a## |
| Change in concentration | - | ##+q## | ##+q## |
| Equilibrium concentration | - | ##a+p+q## | ##a+q## |
Thus, we can obtain the following expressions at equilibrium. $$K_w=\left(a+p+q\right)\left(a+q\right)$$ $$K_a=\dfrac{\left(a+p+q\right)\left(p\right)}{c-p}$$ Taking ##r=a+q##, we obtain the following cubic equations in ##p## and ##r##. $$p^3K_a+p^2\left(K_a^2−K_w−cK_a\right)−2pcK_a^2+c^2K_a^2=0$$ $$r^3K_a+r^2\left(cK_a+K_w\right)−rK_aK_w−K_w^2=0$$ Now, as the acid begins to dissociate, because there is ##\text{H}_3\text{O}^+## already present in the system, the reverse "association" process should start off faster, so it should take lesser time for its rate to increase up to a significant value bringing the system to equilibrium, allowing time only for fewer molecules of the acid to dissociate.
At the same time, because ##\text{H}_3\text{O}^+## is being "removed" by the reverse autoionization process as it forms, the system should be trying to keep the ##\text{H}_3\text{O}^+## concentration below whatever value it would otherwise have risen to in the absence of autoionization.
The fact that the reverse autoionization process is triggered as the reaction proceeds should mean that ##\text{OH}^-## ions in the system should be being consumed, so by the time equilibrium is attained, its concentration must be lesser than the initial value. This means that ##r## in the equation above must be less than ##a##, so if ##a## can be considered small, then ##r^3## must be even smaller, and the effect of the ##r^3## term in the equation should be negligible. It should therefore be possible the reduce it to $$r^2\left(cK_a+K_w\right)−rK_aK_w−K_w^2=0$$ The following is a plot I made of the above equations with the ##x## axis representing ##c## and ##y## axis representing ##r##. The ##r^3## term is neglected in the orange curve, and not neglected in the black curve (##K_a=5## and ##K_w=0.5## here).
The orange curve greatly deviates from the black curve for small concentrations. Is this possible, because ##r## must always be less than ##a## for all concentrations? Have I made an error somewhere? Is it wrong to neglect the ##r^3## term?
By the way, I have not seen calculations being made taking the ##\text{H}_3\text{O}^+## and ##\text{OH}^-## concentrations already present in the system initially into consideration. Where the autoionization of water is not neglected it is always assumed that there are no ##\text{H}_3\text{O}^+## and ##\text{OH}^-## ions present in the system before equilibrium. Why is this? Is there anything wrong with saying it is already present?
Last edited: