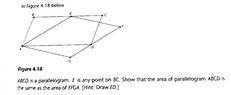
SUMMARY
The forum discussion centers on the area congruence of two quadrilaterals, specifically addressing the relationship between triangle AED and quadrilaterals ABCD and EFGA. The area formulas for triangles, parallelograms, and trapezoids are referenced, emphasizing the need to prove that EFGA is a parallelogram to solve the problem. Participants concluded that without this assumption, the problem remains unsolvable. The author of the book confirmed that the problem statement contained an error, which omitted the necessary definition of EFGA as a parallelogram.
PREREQUISITES
- Understanding of area formulas: Area of a triangle, parallelogram, and trapezoid
- Knowledge of quadrilaterals and their properties
- Familiarity with geometric proofs and assumptions
- Basic algebra for manipulating geometric equations
NEXT STEPS
- Study geometric proofs involving quadrilaterals
- Learn about the properties of parallelograms and how to prove them
- Explore advanced area calculation techniques for complex shapes
- Review common errors in mathematical problem statements and their implications
USEFUL FOR
Students, educators, and mathematicians interested in geometric properties and proofs, particularly those focusing on quadrilaterals and area calculations.