Zula110100100
- 250
- 0
I asked a similar question about gravity, but I would just like to check the math of this first.
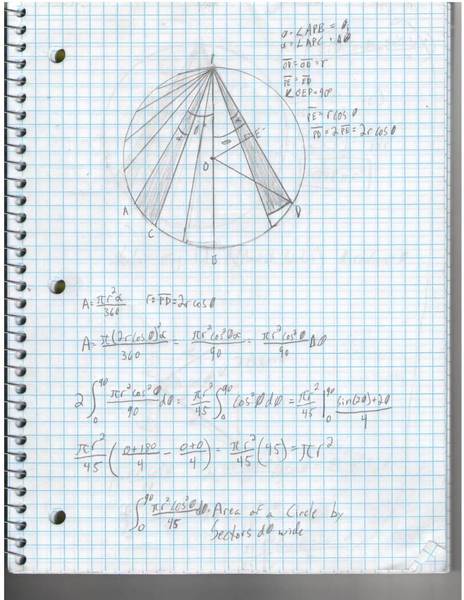
In the first picture I have a circle of radius r, There is a point p on the circle, and I am first trying to show that the equation below gives the area of the circle:
2\int^{90}_{0} \frac{\pi r^2cos^2\theta}{90}d\theta
I got this from the area of a sector of a circle, but rather than from the center, go with the sector of a circle whose radius is a chord. It cuts some off, but as d\theta→0 so does the error.
If you take out the constants and solve, you have:
\frac{\pi r^2}{45}\int^{90}_{0}\cos^2\theta d\theta = \frac{\pi r^2}{45} |^{90}_{0}\frac{sin(2\theta) + 2\theta}{4} = \frac{\pi r^2}{45}(\frac{180}{4}) = \pi r^2
So that gives you the area of a circle figured up by little slices, the angle of each we know, it is \theta, or to be more correct, in each sector there is an angle \theta^{\ast}_{\imath} that points to the center of the area, and as d\theta approaches 0, \theta^{\ast}_\imath approaches \theta
Alright, so if that is all good, then I introduced a vector, whose magnitude was the area of the sector defined above, and whose direction is \theta, relative to a line going through the point and the center, for each slice. I could figure out how much of the area is parallel to a line going from the point P to the center of the circle with:
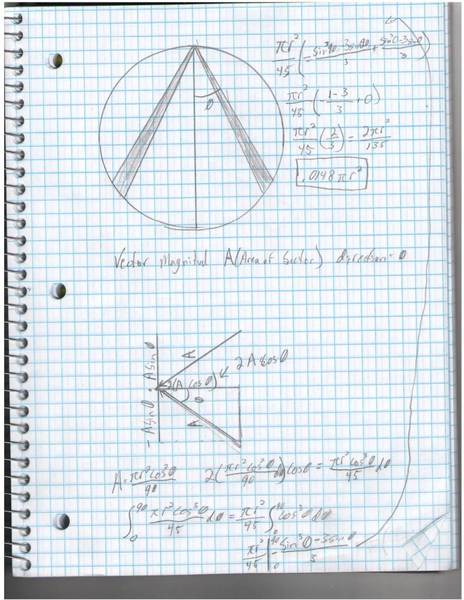
2A\cos \theta
Substituting in for A we get:
\int^{90}_{0}\frac{\pi r^2\cos^3\theta}{45}d\theta
As before pull out the constants and evaluate:
\frac{\pi r^2}{45}\int^{90}_{0}cos^3\theta d\theta = \frac{\pi r^2}{45}|^{90}_{0}-\frac{\sin^3\theta -3\sin\theta}{3} = \frac{\pi r^2}{45}(\frac{2}{3}) = .0\overline{148}\pi r^2
This this math correct? Is there only 1.\overline{481}\% of the circle "parallel to" a line going from the center to a point on the circumference?
In the first picture I have a circle of radius r, There is a point p on the circle, and I am first trying to show that the equation below gives the area of the circle:
2\int^{90}_{0} \frac{\pi r^2cos^2\theta}{90}d\theta
I got this from the area of a sector of a circle, but rather than from the center, go with the sector of a circle whose radius is a chord. It cuts some off, but as d\theta→0 so does the error.
If you take out the constants and solve, you have:
\frac{\pi r^2}{45}\int^{90}_{0}\cos^2\theta d\theta = \frac{\pi r^2}{45} |^{90}_{0}\frac{sin(2\theta) + 2\theta}{4} = \frac{\pi r^2}{45}(\frac{180}{4}) = \pi r^2
So that gives you the area of a circle figured up by little slices, the angle of each we know, it is \theta, or to be more correct, in each sector there is an angle \theta^{\ast}_{\imath} that points to the center of the area, and as d\theta approaches 0, \theta^{\ast}_\imath approaches \theta
Alright, so if that is all good, then I introduced a vector, whose magnitude was the area of the sector defined above, and whose direction is \theta, relative to a line going through the point and the center, for each slice. I could figure out how much of the area is parallel to a line going from the point P to the center of the circle with:
2A\cos \theta
Substituting in for A we get:
\int^{90}_{0}\frac{\pi r^2\cos^3\theta}{45}d\theta
As before pull out the constants and evaluate:
\frac{\pi r^2}{45}\int^{90}_{0}cos^3\theta d\theta = \frac{\pi r^2}{45}|^{90}_{0}-\frac{\sin^3\theta -3\sin\theta}{3} = \frac{\pi r^2}{45}(\frac{2}{3}) = .0\overline{148}\pi r^2
This this math correct? Is there only 1.\overline{481}\% of the circle "parallel to" a line going from the center to a point on the circumference?