Calculating the surface area of a sphere using dA

[annamal]

TL;DR Summary

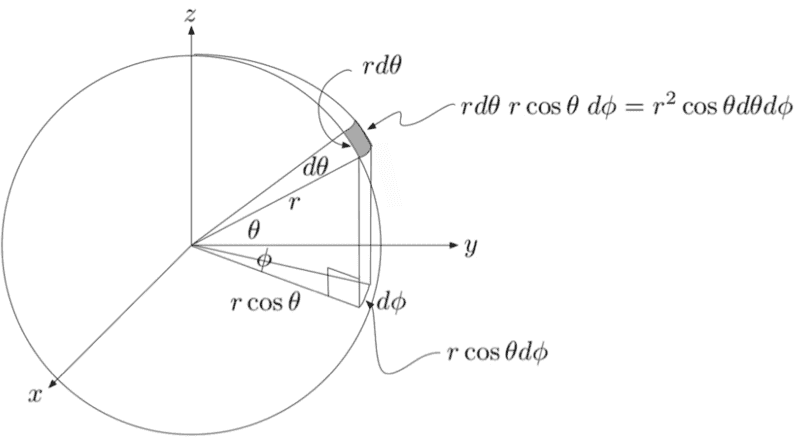
I am confused by the surface area of a sphere using dA. Not sure why the other side can't just be $Rd\phi$

Below is an image to calculate the surface area of a sphere using dA. I can see how $rcos\theta d\phi$ works, but I don't understand how that side can't just be $rd\phi$ with a slanted circle representing the arc length. The second part I don't understand is why it is integrated from $\frac{\pi}{2}$ to $\frac{-\pi}{2}$

 

[anuttarasammyak]

Summary:: I am confused by the surface area of a sphere using dA. Not sure why the other side can't just be $Rd\phi$

I can see how rcosθdϕ works,

$$r\sin\theta d\phi$$
isn't it ? Usually $\theta$ is measured from z axis, not from xy plane. And the side is
$$r d\theta$$

 

[annamal]

$$r\sin\theta d\phi$$
isn't it ? Usually $\theta$ is measured from z axis, not from xy plane. And the side is
$$r d\theta$$

That is not answering my question. I am naming them based on the image attached.

 

[anuttarasammyak]

Then apply to post#2 which uses $\theta_{ordinary} [0,\pi]$, the transformation,
$$\theta_{yours}=\frac{\pi}{2}-\theta_{ordinary}$$ which would give what you want.

 

[annamal]

Then apply to post#2 which uses $\theta_{ordinary} [0,\pi]$, the transformation,
$$\theta_{yours}=\frac{\pi}{2}-\theta_{ordinary}$$ which would give what you want.

I am not sure where you got the yours and mine...could you explain in more detail?

 

[anuttarasammyak]

In ordinary polar coordinates,
$$dA= r^2 \sin \theta dr d\theta d\phi$$
$$\theta[0,\pi],\phi[0,2\pi]$$
Substitute here

$$\theta_{yours}=\frac{\pi}{2}-\theta_{ordinary}$$

Your $\theta$ is same as latitude in global positioning with - for south and + for north.

 

[Antarres]

The reason $\theta$ is integrated from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$ is because that's how you define it in the picture, $\theta$ is an angle that goes from south to north pole of the sphere as I see it.

As for your question regarding why do you need a cosine factor in your case, why not just $rd\phi$, I would suggest this kind of experiment. Imagine you fix $\theta$, and you want to calculate the surface of one 'ring' that is elevated at $\theta$ from the surface. The surface of that ring, you should get if you don't integrate over $\theta$ but just over $\phi$, right? But if you do that you will find that the surface of such ring would be $2r\pi \cdot rd\theta$. And that can't be correct, right, the ring's circumference is not $2r\pi$ above the equator, it is $2r\pi\cos\theta$. So that's why you need that factor, it includes the change of size of those rings because of the curvature of the sphere.

 

[annamal]

The reason $\theta$ is integrated from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$ is because that's how you define it in the picture, $\theta$ is an angle that goes from south to north pole of the sphere as I see it.

As for your question regarding why do you need a cosine factor in your case, why not just $rd\phi$, I would suggest this kind of experiment. Imagine you fix $\theta$, and you want to calculate the surface of one 'ring' that is elevated at $\theta$ from the surface. The surface of that ring, you should get if you don't integrate over $\theta$ but just over $\phi$, right? But if you do that you will find that the surface of such ring would be $2r\pi \cdot rd\theta$. And that can't be correct, right, the ring's circumference is not $2r\pi$ above the equator, it is $2r\pi\cos\theta$. So that's why you need that factor, it includes the change of size of those rings because of the curvature of the sphere.

I drew a picture. It seems like the ring's circumference is $2r\pi$ according to my drawing (in red).

 

[anuttarasammyak]

No, it doesn’t fit the curve. Horizontal circle centered on z axis of radius r cos $\theta$ does. Vertical red circles fit the sides. Ref. https://en.m.wikipedia.org/wiki/File:FedStats_Lat_long.svg

 

[annamal]

No, it doesn’t fit the curve. Horizontal circle centered on z axis of radius r cos $\theta$ does. Vertical red circles fit the sides. Ref. https://en.m.wikipedia.org/wiki/File:FedStats_Lat_long.svg

I am confused. In the picture the red circle seems to fit the curve.

 

[anuttarasammyak]

 

[annamal]

View attachment 300524

Yes, I understand the red and blue circles you drew. My question is why the red circle I drew in my image is not right.

 

[anuttarasammyak]

My question is why the red circle I drew in my image is not right.

Imagine you cut globe or watermelon with knife at near its north pole and get a small circle intersection.
Do you still think that red circle fits this small cross section circle ?

 

[annamal]

Imagine you cut globe or watermelon with knife at near its north pole and get a small circle intersection.
Do you still think that red circle fits this small cross section circle ?

No, but that is not what I am asking. I am asking why that side of the dA cannot be the red circle I drew.

 

[anuttarasammyak]

You admit blue circles fit the top/bottom side of the element. Are you expecting another circle e.g. red one fit these sides also and it is possible ?

 

[annamal]

You admit blue circles fit the top/bottom side of the element. Are you expecting another circle e.g. red one fit these sides also and it is possible ?

From the drawing it seems possible.

 

[anuttarasammyak]

Can you draw it for the case of post #13 though you said no in #14 ?

 

[annamal]

Can you draw it for the case of post #13 though you said no in #14 ?

The blue and red circles seem to indicate the same dx

 

[anuttarasammyak]

The blue and the red cross at the point. The do not share the arc side of the element to fit. As I said smaller radius blue circle case or in other words near pole cross section case would show it to us clearly. In the case of equator only they coincide.

If two or more circles fit the same curve, we could not define unique curvature of the curve which is defined as reciprocal of such a circle.

 

[annamal]

The blue and the red cross at the point. The do not share the arc side of the element to fit. As I said smaller radius blue circle case or in other words near pole cross section case would show it to us clearly. In the case of equator only they coincide.

If two or more circles fit the same curve, we could not define unique curvature of the curve which is defined as reciprocal of such a circle.

Yes, I know they are not same curve. My thread is asking why I can't just use the red circle's arc as dx.

 

[anuttarasammyak]

Do you mean not only $\phi$ but also $\theta$ plays the role of longitude as in right side figure of https://en.m.wikipedia.org/wiki/File:FedStats_Lat_long.svg ?
If so the lines do not intersect perpendicularly. I see a clear uneasiness at the poles.

 

[annamal]

Do you mean not only $\phi$ but also $\theta$ plays the role of longitude as in right side figure of https://en.m.wikipedia.org/wiki/File:FedStats_Lat_long.svg ?
If so I see an uneasiness at the poles.

What do you mean here?

 

[anuttarasammyak]

Please find attach figure on the coordinates system that I assume your red-circle requirement in #8 could be satisfied. Not mentioned in the figure but you see there exist East pole and West pole as well as NS poles. The curves $\theta=const.\ \ \phi=const.$ do not intersect perpendicularly. It complicates the calculation of dA.

 

[renormalize]

Your red circle is tilted relative to the $xy$ ($\theta=\frac{\pi}{2}$) plane. But the standard approach to calculate the surface area of a sphere uses surface slices which are all parallel to the $xy$ plane (like anuttarasammyak's blue circle). The infinitesimal surface area of each slice is $2\pi r^{2}\sin\left(\theta\right)d\theta$ and varies according to the height $r\cos\left(\theta\right)$ of the slice above or below the $xy$ plane. As shown below, you then stack up all the parallel slices and add up their areas (by integration over $\theta$) to get the total surface area $4\pi r^{2}$ of the sphere.

 

[annamal]

Your red circle is tilted relative to the $xy$ ($\theta=\frac{\pi}{2}$) plane. But the standard approach to calculate the surface area of a sphere uses surface slices which are all parallel to the $xy$ plane (like anuttarasammyak's blue circle). The infinitesimal surface area of each slice is $2\pi r^{2}\sin\left(\theta\right)d\theta$ and varies according to the height $r\cos\left(\theta\right)$ of the slice above or below the $xy$ plane. As shown below, you then stack up all the parallel slices and add up their areas (by integration over $\theta$) to get the total surface area $4\pi r^{2}$ of the sphere.
View attachment 300589

Why can't the red circle be tilted though

 

[annamal]

Please find attach figure on the coordinates system that I assume your red-circle requirement in #8 could be satisfied. Not mentioned in the figure but you see there exist East pole and West pole as well as NS poles. The curves $\theta=const.\ \ \phi=const.$ do not intersect perpendicularly. It complicates the calculation of dA.
View attachment 300588View attachment 300592

Yes, I see and understand that but if we tilted the circle, why can't that be a side to dA?

 

[PeterDonis]

if we tilted the circle, why can't that be a side to dA?

It could, if you were able and willing to change all of your formulas so that they did not have built into them the convention that the circles are all lined up a certain way. This convention does not sacrifice any generality: it amounts to lining up the coordinates a certain way on the sphere to make the computation easy.

The diagram you show in your OP does use the convention that the circles are all lined up a certain way, and all of the math that has been discussed in this thread is based on that convention. So you can either use the math you have been shown, which works and is easy, or you can make the problem much, much harder (and have to start over working it from scratch) by refusing to adopt a simple convention that makes the math easy.

Your call.

 

[annamal]

It could, if you were able and willing to change all of your formulas so that they did not have built into them the convention that the circles are all lined up a certain way. This convention does not sacrifice any generality: it amounts to lining up the coordinates a certain way on the sphere to make the computation easy.

The diagram you show in your OP does use the convention that the circles are all lined up a certain way, and all of the math that has been discussed in this thread is based on that convention. So you can either use the math you have been shown, which works and is easy, or you can make the problem much, much harder (and have to start over working it from scratch) by refusing to adopt a simple convention that makes the math easy.

Your call.

Ok, that makes sense. Why aren't we integrating that from 0 to 2*pi? But -pi/2 to pi/2?

 

[PeterDonis]

Why aren't we integrating that from 0 to 2*pi? But -pi/2 to pi/2?

We are integrating over $\theta$, i.e., latitude, which goes from $- \pi / 2$ at the south pole to $+ \pi / 2$ at the north pole.

 

[annamal]

We are integrating over $\theta$, i.e., latitude, which goes from $- \pi / 2$ at the south pole to $+ \pi / 2$ at the north pole.

To be a full circle, doesn't it have to be 2pi? See image.

 

[jedishrfu]

Perhaps this bideo from 3blue1brown will give you a different perspective on the sphere

 

[PeterDonis]

To be a full circle

When you go from the South Pole to the North Pole, you only go through half a circle, not a full circle. That is what the integral we are talking about is doing. It is adding up the areas of infinitesimal circular "slices" of the Earth's surface, each "slice" taken at a different latitude, over the full range of latitudes from the South Pole to the North Pole. The area of each infinitesimal slice is the circumference of the circle at latitude $\theta$, which is $2 \pi r \cos \theta$, times the infinitesimal width of the slice, which is $r d \theta$. So we are integrating $2 \pi r^2 \cos \theta d \theta$ from $\theta = - \pi / 2$, the South Pole, to $\theta = \pi / 2$, the North Pole.

 

[anuttarasammyak]

To be a full circle, doesn't it have to be 2pi?

If you wonder about polar coordinates that includes a modified verion of measuring $\theta$ from xy plane not from usual z axis, you can see many explanations in school texts and web contents. Peter also has done a good explanation in the previous post.

If you question about coordinates system that I said in post #23 the figure of which you quoted, imagine as follows.
Imagine all the curves mentioning constant longitude spanning between the North pole and the South pole in your mind.
Imagine the equator circle is made of sponge wet with red ink. Turn it gradually along the East pole - the West pole axis. You see those curves are getting painted red left after the equator circle passes. How much angle should the equator circle turn to paint all parts of those curves ?
And how about it when not the full equator circle but only a half equator circle between EW axis sponge is wet ?
Colored red points on the globe surface have been shown already appointed by the coordinates.

 

[annamal]

If you wonder about polar coordinates that includes a modified verion of measuring $\theta$ from xy plane not from usual z axis, you can see many explanations in school texts and web contents. Peter also has done a good explanation in the previous post.

If you question about coordinates system that I said in post #23 the figure of which you quoted, imagine as follows.
Imagine all the curves mentioning constant longitude spanning between the North pole and the South pole in your mind.
Imagine the equator circle is made of sponge wet with red ink. Turn it gradually along the East pole - the West pole axis. You see those curves are getting painted red left after the equator circle passes. How much angle should the equator circle turn to paint all parts of those curves ?
And how about it when not the full equator circle but only a half equator circle between EW axis sponge is wet ?
Colored red points on the globe surface have been shown already appointed by the coordinates.

I get it now. Thank you!