I_am_learning
- 681
- 16
Finding the area of an irregular polygon with n side is quite easy when we are given the length of all of the n sides and the length of (n-3) specific diagonals. This way, we get (n-2) triangles whose areas can be calculated using Heron's formula and then added up.
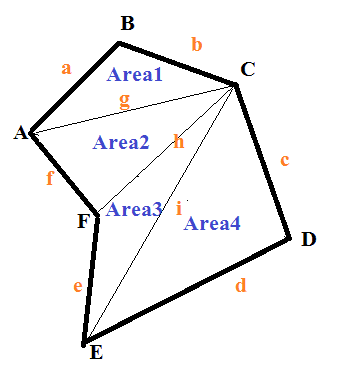
But what if the length of the (n-3) diagonals provided doesn't make (n-2) triangles, such as this case:
The polygon is still fully determined by the given measurements, but calculating the area is difficult.
Is there some sort of generic formula for such cases? Like maybe using matrices. :D
I thought of making a mobile application to help real-estates peoples calculate the area of lands, and came-up with this question.
Thank you.
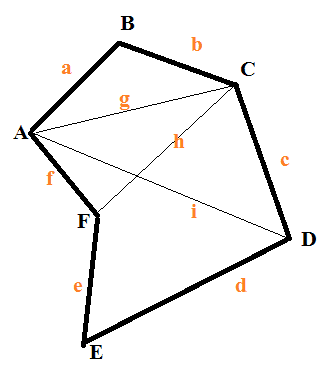
But what if the length of the (n-3) diagonals provided doesn't make (n-2) triangles, such as this case:
The polygon is still fully determined by the given measurements, but calculating the area is difficult.
Is there some sort of generic formula for such cases? Like maybe using matrices. :D
I thought of making a mobile application to help real-estates peoples calculate the area of lands, and came-up with this question.
Thank you.