Calculating the Area of an Apollonian Gasket: A Formula for n Layers

[caters]

Here is my formula for the area of n layers of appolonian gasket(assuming no circles past the nth layer):

$$πR^2 - (πR^2 - (\sum_{0}^{n} x_n*πr_{n}^2))$$

Here R is the radius of the outer circle, r is the radius of an inner circle, x is a function that represents the number of circles in a given layer and n is the number of layers.

I know this is right as far as calculating area is concerned but how would I actually represent this if I wanted to show someone else this formula?

The reason I only have $πr_{n}^2$ once is because here is what the sum would be like for a successive number of layers. If I assume I have this kind of Apollonian gasket:

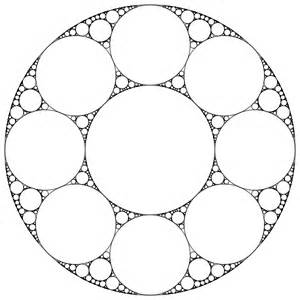
then the area formula is like this as n increases:

n=0

$$πR^2 - (πR^2 - (πR^2)) = πR^2$$

n=1

$$πR^2 - (πR^2 - (πr_{1}^{2}))$$

n=2

$$πR^2 - (πR^2 - (πr_{1}^2 + 8*πr_{2}^2))$$

n=3

$$πR^2 - (πR^2 - (πr_{1}^2 + 8*πr_{2}^2 + 8*πr_{3}^2))$$

etc.

But I could easily replace each of those multipliers with $x_1$, $x_2$, $x_3$ etc.

So basically every time n increases by 1 is a time when the radius changes in an Apollonian gasket as you get more and more circles inside that 1 outer circle.

Would the general formula for any Apollonian gasket I have at the top of this post be the best way to represent this area formula?

 

[zinq]

I'm not sure how "layers" is being defined. I would have guessed that a disk of the n+1^st layer is one that is as large as possible inside one of the gaps left by the n^th layer.

But if so, then beginning with n = 3 (i.e., in the 3^rd layer), the radii of its disks are not just a function of n. So I am not sure if I understand the definition of what the n^th layer is.

 

[caters]

The way I am defining it here is that when n = 0, the resulting formula is just the area of the outer circle. x I am defining here as a function that represents how many circles there are of a given radius at n.

In the n =/ 0 case, n represents the number of radii that aren't the radius of the outer circle. so when n = 3, there are 3 radii that aren't the radius of the outer circle. As n increases, the number of different radii increases in a 1:1 ratio. So it is the number of radii, not the radii themselves that n represents. The radii are defined in a geometric and trigonometric way.

 

[zinq]

I'm not asking how many, but how is the "next layer" defined?

 

[caters]

And the next layer is defined by a change in radius as you go either outwards or inwards. I myself would do it so that inward and outward layers alternate. So I would have at n = 4, the center circle radius, tangent circle radius, first outward layer(touches the largest tangent circles but itself isn't tangent to the outer circle), and first inward layer(same touching tangent circles but this time not being tangent to the center circle instead) for at least this kind of Apollonian gasket and in general for any Apollonian gasket, the next layer would be defined by the next smallest radius.

 

[zinq]

How about n=3 ?

 

[caters]

For n = 3, in the kind of Apollonian gasket shown here the radii in that sum would be the center circle radius, tangent circle radius, and then the next smallest radius after that which is outwards from the tangent circles but itself isn't tangent to the outer circle. So in general, as n increases, the nth radius gets smaller and smaller and as n approaches infinity, the nth radius approaches 0 and the area of the Apollonian gasket approaches the area of the outer circle.

 

[zinq]

I am still very confused. Let's call the biggest disk — the "whole thing" — D(0).

Consider the "first" layer — the single largest disk D(1) (not counting the whole thing), centered at the center of the whole thing.

I will call the "second" layer the 8 disks that are tangent to D(1) and (internally) to D(0). We can call these the 8 D(2)'s

Now look at the disks having the largest remaining radius. These are each tangent to 2 of the D(2)'s, but lie between them and D(0), without being tangent to D(0).

I have no idea how these disks, which you would apparently call the third layer, are defined. Can you please explain?