SUMMARY
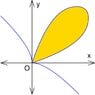
The discussion focuses on calculating the area of the loop defined by the equation ##x^5 + y^5 = 3x^2y^2## using polar coordinates. The area is derived using the formula ##A = \frac{1}{2} \int_0^{\pi/2} \left[\frac{3\cos^2\theta \sin^2\theta}{\cos^5\theta + \sin^5\theta}\right]^2 d\theta##, which simplifies to ##A = 0.9##. Participants also discuss various substitutions and transformations, including using Green's theorem to set up the area calculation.
PREREQUISITES
- Understanding of polar coordinates and transformations
- Familiarity with calculus, specifically integration techniques
- Knowledge of Green's theorem and its application in area calculations
- Proficiency in handling complex algebraic expressions and substitutions
NEXT STEPS
- Study the application of Green's theorem in calculating areas of complex shapes
- Learn about polar coordinate transformations and their implications in calculus
- Explore advanced integration techniques, including substitutions and integration by parts
- Investigate the properties and applications of the folium of Descartes curve
USEFUL FOR
Mathematicians, calculus students, and anyone interested in advanced geometry and area calculations in polar coordinates.