Help seeker
- 15
- 0
Figure shows six identical circles inside a rectangle.
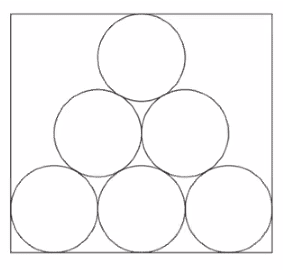
The radius of each circle is 24 cm. The radius of the circles is the greatest possible radius so that the circles fit inside the rectangle. The six circles form the pattern shown in Figure so that
• each circle touches at least two other circles
• the circle in the top row of the pattern and the circles in the bottom row of the pattern touch at least one side of the rectangle
• the centres of the circles all lie on the perimeter of a single triangle.
Find the total area of the $six$ $circles$ $as$ $a$ $percentage$ $of$ $the$ $area$ $of$ $the$ $rectangle$.
The radius of each circle is 24 cm. The radius of the circles is the greatest possible radius so that the circles fit inside the rectangle. The six circles form the pattern shown in Figure so that
• each circle touches at least two other circles
• the circle in the top row of the pattern and the circles in the bottom row of the pattern touch at least one side of the rectangle
• the centres of the circles all lie on the perimeter of a single triangle.
Find the total area of the $six$ $circles$ $as$ $a$ $percentage$ $of$ $the$ $area$ $of$ $the$ $rectangle$.