bluskies
- 11
- 0
Homework Statement
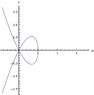
Find the area of the plane region bounded by the curve
$$
(x^2+y^2)^3 = x^4+y^4
$$
Homework Equations
The change of variables formula:
$$
\int\int_R F(x,y)dxdy = \int\int_S G(u,v)\left| \frac{∂(x,y)}{∂(u,v)}\right| dudv
$$
The Attempt at a Solution
I recognize this as a change of variables problem, and in general I understand how to do change of variables, but for this one I cannot figure out what to use as the new variables u = u(x,y) and v = v(x,y). Previously I could tell what I needed by inspection, but I cannot tell with this problem. Is there some method for directly computing what u and v must be?
I thought of using {u = x^2 + y^2} and {v = x^4 + y^4}, but I can't figure out how to use this to solve for x and y, so I reached a dead end.
Any help would be appreciated.