At what frequency can Planck's law be used to determine the temperature?

[Lambda96]

Homework Statement

Use the expression for the Planck function in the Rayleigh-Jeans approximation and estimate to which frequencies it can be used to determine the temperature of an astronomical source of temperature 20 K. Use the first two terms in the Taylor-series from the lecture and assume 10% relative accuracy.

Relevant Equations

T-h*f/2*k T=Temperature, h=Planck constant, f=Frequency , k=Boltzmann constant

Hi,

I am not quite sure if I have calculated the homework correctly :-)

I proceeded in such a way that I first calculated from which frequency the two terms are equal, and thus the equation results in zero.

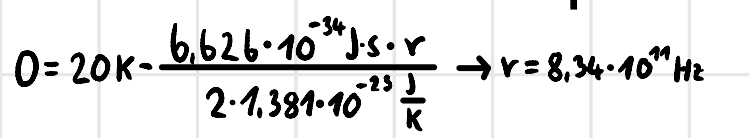
Then I figured a relative accuracy of 10% equals a relative error of 90%. So I calculated at which frequency I have a relative error of 90% and exactly this frequency is the one I am looking for.

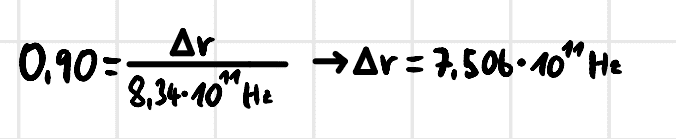
Am I thinking correctly, or am I completely wrong? :-)

 

[haruspex]

I don’t understand the question.

I presume the Taylor series is for the exponential term in the Planck formula. Taking just the first two terms of that leads to the Rayleigh–Jeans approximation.

You quote an expression T-h*f/2*k. You don't say what that is a formula for, but setting it to zero does not sound promising.

But then, I do not see how knowing the intensity at a single frequency can be used to estimate a temperature. You would need two at least.

 

[Steve4Physics]

I think the question means this...

The Rayleigh -Jeans law predicts that for a body at temperature T, the radiance of frequency f (or $\nu$ if preferred) is some function of f and T: $B_{RJ}(f, T)$.

Planck’s law predicts that for a body at temperature T, the radiance of frequency f is a different function of f and T: $B_P(f, T)$.

It turns out that $B_{RJ}(f, T) > B_P(f, T)$. The difference $B_{RJ} - B_P$ gets bigger as f increases (keeping T constant). (And $B_{RJ}$ gets impossibly large as frequency continues to increase.)

For an object at temperature T = 20K, I think a 10% (=0.1) relative accuracy means
$\frac {B_{RJ} – B_P}{B_P}= 0.1$

So you need to replace $B_{RJ}$ and $B_P$ by suitable expressions (functions of f and T, possibly aproxinations), set T=20K and solve for f.

 

[Lambda96]

Thanks haruspex and Steve4Physics for your help. I asked my lecturer again, and he said that I only need this formula T - h*f/2*k to solve the problem. Unfortunately, he did not tell me more :-)

 

[Steve4Physics]

Thanks haruspex and Steve4Physics for your help. I asked my lecturer again, and he said that I only need this formula T - h*f/2*k to solve the problem. Unfortunately, he did not tell me more :-)

T - h*f/2*k is not a formula, there is no '=' sign. It is an expression and you haven't told us what it means or equals. (Note what @haruspex said in Post #2.)

Also, the expression could use some brackets to avoid ambiguity but I guess it is $T - \frac {hf}{2k}$. so it is some sort of temperature or temperature-difference. But I don't recognise it.

 

[haruspex]

Thanks haruspex and Steve4Physics for your help. I asked my lecturer again, and he said that I only need this formula T - h*f/2*k to solve the problem. Unfortunately, he did not tell me more :-)

Following @Steve4Physics' insight in post #3, we should take the first three terms of the expansion of the exponential in the denominator of Planck's formula. The first, 1, cancels with the -1 in the denominator. This leaves a factor $\frac 1{\frac{h\nu}{kT}+\frac 12(\frac{h\nu}{kT})^2}=\frac{kT}{h\nu}(1+\frac 12\frac{h\nu}{kT})^{-1}\approx\frac{kT}{h\nu}-\frac 12$.

The Rayleigh–Jeans approximation is the same but without the $-\frac 12$. So the question becomes, at what temperature does the R-J version diverge by 10%? If you juggle the equations you will find it is when the formula quoted in post #1 differs from T by 10%.