chwala
Gold Member
- 2,828
- 425
- Homework Statement
- See attached.
- Relevant Equations
- differentiation.
I had to look this up; will need to read on it.
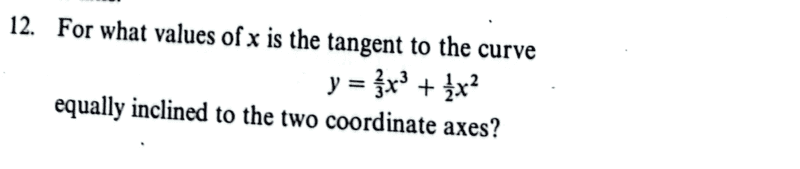
from my research,
https://byjus.com/question-answer/t...om-the-points-1-2-and-3-4-is-ax-by-c-0-where/
...
I have noted that at equally inclined; the slope value is ##1##.
##\dfrac{dy}{dx} = 2x^2+x=1##
##2x^2+x-1=0##
##x=-1## or ##x=0.5##
the steps are clear; but i need to understand the concept...i guess more reading on my part. ...just sharing in the event one has insight to offer. Cheers.
from my research,
https://byjus.com/question-answer/t...om-the-points-1-2-and-3-4-is-ax-by-c-0-where/
...
I have noted that at equally inclined; the slope value is ##1##.
##\dfrac{dy}{dx} = 2x^2+x=1##
##2x^2+x-1=0##
##x=-1## or ##x=0.5##
the steps are clear; but i need to understand the concept...i guess more reading on my part. ...just sharing in the event one has insight to offer. Cheers.