Atom Self Capacitance: Electron Energy Levels

[edguy99]

The empty shell provokes some interesting thought when considering the orbit of an electron. Assume there is no proton/electron coulomb force if the electron is inside the proton shell.

Some simulations. First is an electron orbiting a proton with enough energy that it gets a reasonable orbit. The second simulation shows a lower energy electron completely trapped within the proton. The third simulation shows the kind of orbits you get with more objects (two electons and one proton).

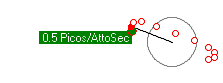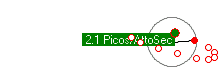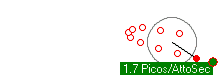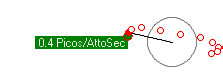[PLAIN]http://upload.wikimedia.org/wikipedia/commons/7/7c/Protonelectrontrapped.gif[ATTACH=full]196589[/ATTACH][/URL]

 

[Vanadium 50]

Assume there is no proton/electron coulomb force if the electron is inside the proton shell.

But that's demonstrably not true. You have proton-electron scattering experiments, and you have atomic spectra: particularly with muonic atoms. (Jim Rainwater always felt the Nobel committee gave him the Nobel prize for the wrong thing, and that he should have gotten it for muonic atoms)

 

[edguy99]

But that's demonstrably not true. You have proton-electron scattering experiments, and you have atomic spectra: particularly with muonic atoms. (Jim Rainwater always felt the Nobel committee gave him the Nobel prize for the wrong thing, and that he should have gotten it for muonic atoms)

It is correct that scattering experiments suggest a proton size of 1-2 femtometers, not 53,000 femtometers (53 pm) as drawn here. It suggests in this type of model that the large shells have a thickness to them of 1-2 femtometers. Protons only really "crash" into each other if they are centered almost exactly on top of each other.

In other words, in this type of world, proton shells can overlap each other and often would. Normal forces continue to push the protons apart even if they are overlapping. Electrons caught in the overlapping shells are the "glue" that hold the protons together.

 

[nuby]

Something else I found interesting using this 'model'.

Using the Rydberg constant you can figure out the moment of inertia:

KE_electron = (1/2) * electron_mass * (fine_structure_constant * c)^2 = 13.605 eV
or

KE_rotational = (1/2) * I * w^2 = 13.605 eV

w = angular velocity = 6.57968395e15 * 2 * pi = 4.134e16 rads/sec
I = moment of inertia = 2.55075e-51

The moment of inertia for a thin circular hoop is: I(z_axis) = mass * radius^2
I = electron_mass * bohr_radius^2 = 2.55088e-51

This view seems to depict the electron shell as a 2D hoop (in a single frame).Another thing I thought was interesting:
The coulombs force between the proton and electron in ground state hydrogen:

F(coulombs) = (1/(4*pi*electric_constant)) * elementary_charge^2/bohr_radius^2
F(coulombs) = 8.2387e-8 N

The centripetal force of the ground state hydrogen: m * (velocity^2 / bohr_radius)
F(centripetal) = electronmass * (fine_structure_constant * c)^2 / bohr_radius
F(centripetal) = 8.2387e-8 N

 

[Vanadium 50]

It is correct that scattering experiments suggest a proton size of 1-2 femtometers, not 53,000 femtometers (53 pm) as drawn here. It suggests in this type of model that the large shells have a thickness to them of 1-2 femtometers. Protons only really "crash" into each other if they are centered almost exactly on top of each other.

In other words, in this type of world, proton shells can overlap each other and often would. Normal forces continue to push the protons apart even if they are overlapping. Electrons caught in the overlapping shells are the "glue" that hold the protons together.

Is this model described in the literature anywhere? This doesn't sound like the conventional description.

 

[Vanadium 50]

Nuby, for a classical orbit the centripetal acceleration is equal to the central force acceleration.

Let me repeat - in all of these, what you are discovering is that when you put the Rydberg constant in, you can get it out again. Nothing more, nothing less.

 

[nuby]

The Lorentz force also came out to have a value right around: 2 * 8.2387e-8 N.

 

[edguy99]

Is this model described in the literature anywhere? This doesn't sound like the conventional description.

I don't know that it would be conventional. Its core is the description of the hydrogen proton as an empty shell of charge (53pm) and seeing what can and cannot be explained.

I do computer animations and use the rules I call the http://en.wikipedia.org/wiki/User:Edguy99" .

 

[Vanadium 50]

Nuby, again, what you are discovering is that when you put the Rydberg constant in, you can get it out again. There's no physics in this - it's all algebra.

You may not be aware of it, but a great many cranks "discover" these relationships and use them to promote their own particular variety of crackpottery. Because of this, the net effect on your audience is probably more negative than you would think at first.

 

[nuby]

The coulombs force and centripetal force relationship is part of the Bohr model.

Vanadium 50, no crackpot promotions in my posts just questions about the theoretical classical hydrogen model. I understand what you are saying put the Rydberg constant in, and get it back out, and that's just algebra. But you haven't talked about why the values/units are coming together the way they are. For example, if the Bohr Radius of hydrogen wasn't ever discovered but the radius of ground state hydrogen was measured to be 53 pm. With that number alone and some physical constants, you can calculate a lot of the hydrogen atom's real properties. Why is this?

 

[Vanadium 50]

But you haven't talked about why the values/units are coming together the way they are.

The units come out right because they have to. If I take a length and divide it by a time, I have to get units of velocity: even if the length and time have nothing to do with each other.

For example, if the Bohr Radius of hydrogen wasn't ever discovered but the radius of ground state hydrogen was measured to be 53 pm.

Yes, but the Bohr radius would still exist even if it weren't discovered. (And, by the way, a hydrogen atom doesn't actually have a radius: the electron density continually increases the closer to the proton that you get) It's a mathematical construct. But what I am trying to tell you is that the reason all these relationships exist is that there is only one constant - all the others are algebraic manipulations of it.

 

[Reality_Patrol]

The coulombs force and centripetal force relationship is part of the Bohr model.

Vanadium 50, no crackpot promotions in my posts just questions about the theoretical classical hydrogen model. I understand what you are saying put the Rydberg constant in, and get it back out, and that's just algebra. But you haven't talked about why the values/units are coming together the way they are. For example, if the Bohr Radius of hydrogen wasn't ever discovered but the radius of ground state hydrogen was measured to be 53 pm. With that number alone and some physical constants, you can calculate a lot of the hydrogen atom's real properties. Why is this?

Nuby,

I have to agree with V50. All of your calculations are really algebraic identities.
This means there's no new information in them.

The reason I tried to point you in the direction of the paper you found, is because it avoids this dilemma. It's "new" theory, and does not put the Rydberg constant in - in fact it derives it. Many of the relationships you point out could also be derived from that model in new and interesting ways. It's really the way to go if you want to extend your hydrogen atom equivalent circuit model interests theoretically. Again, the goal should be at least one novel, testable prediction from the new theory. Something the paper fell short of.

 

[edguy99]

On the chance that I may not quite understand this correctly,

http://en.wikipedia.org/wiki/Josephson_effect

Is it correct to say that

1. if you cook up a mixture of something like YBCO and lay it out in a small circle
2. if you place the circle in a small magetic field

You will get the electrons in the YBCO circle moving back and forth with a periodic motion we would call the frequency. In other words, the higher the magnetic field, the faster the frequency of the back and forth electron motion in the circle until things break down due to too much motion?

 

[Reality_Patrol]

On the chance that I may not quite understand this correctly,

http://en.wikipedia.org/wiki/Josephson_effect

Is it correct to say that

1. if you cook up a mixture of something like YBCO and lay it out in a small circle
2. if you place the circle in a small magetic field

You will get the electrons in the YBCO circle moving back and forth with a periodic motion we would call the frequency. In other words, the higher the magnetic field, the faster the frequency of the back and forth electron motion in the circle until things break down due to too much motion?

I don't see the junction anywhere in your setup. The JE requires a junction.

Of course an AC magnetic field would induce an AC current even in a superconducting loop. You didn't state what kind of magnetic field was used in your setup.

 

[edguy99]

I don't see the junction anywhere in your setup. The JE requires a junction.

Of course an AC magnetic field would induce an AC current even in a superconducting loop. You didn't state what kind of magnetic field was used in your setup.

Thanks for the comment. I was not sure if the junction was needed or it is just a tool for measuring. I am assuming the magnetic field is DC and am interested in the voltage to frequency conversion. Do the electrons actually move across the junction or is there just a back and forth motion up to the junction? Or perhaps in and out of the junction?

 

[Reality_Patrol]

Thanks for the comment. I was not sure if the junction was needed or it is just a tool for measuring. I am assuming the magnetic field is DC and am interested in the voltage to frequency conversion. Do the electrons actually move across the junction or is there just a back and forth motion up to the junction? Or perhaps in and out of the junction?

Yes, the JE is all about the phenomena of electrons "tunneling" through a thin insulator sandwiched between 2 superconductors, so a junction is needed. The current is definitely "across/through" the insulator because DC currents can be produced as opposed to "in and out" as could be argued if only AC currents were produced.

Here's a link to a pdf that should answer your voltage-to-frequency question:

http://www.phys.ufl.edu/~pjh/teaching/phz7427/7427notes/josephson.pdf

 

[nuby]

So form the above atomic views, is there any significance to the orbital (or vibrational?) frequency of hydrogen (6.57e15 hz) with standard atomic models? It's not something I see too often. Is it used in NMR, or ESR?

 

[edguy99]

So form the above atomic views, is there any significance to the orbital (or vibrational?) frequency of hydrogen (6.57e15 hz) with standard atomic models? It's not something I see too often. Is it used in NMR, or ESR?

Hi Nuby,

I feel your calculation on post#3 is an important one regarding the bohr radius. Your calculation in post#6 assumes a certain speed of the electron. This speed is important in the original calculation of the bohr radius, but does not really reflect reality. We would measure lots of things different if electrons were orbiting hydrogen protons at that speed.

What is important about that speed is that any faster and the electron would fly away from the proton, any slower and the electron would crash into the proton. The electron of course does not crash into the proton but hangs around somewhere "mostly" within the bohr radius even though it seems to be going very slow or even "stopped". We can pull it out of this orbital with 13.6evolts of energy regardless of how close the electron "seems" to be to the center.