Atwood machine with variable mass

[titansarus]

Homework Statement

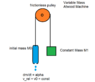
We have an Atwood machine like the picture below. one side (left) is a bucket full of water which has a hole on the bottom and the water is flowing with rate $dm/dt = \alpha = const$. The initial mass of bucket with the water is $m_0$. On the other side (right) we have a box with constant mass $m_1$. We also know the speed of water relative to the system at every time is a constant number $v_0$ (It is given in the question). we want to find the speed of each box (which is equal in opposite directions) at every time $t$. In fact we want to find $v(t)$ ($v$ as a function of $t$).
Note: Pulley and rope and etc... are all frictionless - massless and completely ideal. And the pulley is fixed to somewhere (maybe wall or roof, so it doesn't move)

The Attempt at a Solution

After solving the equations of momentum for an arbitrary system of initial mass $M$, I get the formula
$M dv/dt = F_{ext} + v_{rel}~~ dm/dt$.

in this question $v_{rel}$ and $dm/dt$ are both known constants. But I don't know what to do with $F_{ext}$. Is it for the whole system? Is it just for the bucket? What is $M$ in the question: $m_0$ or $m_0 + m_1$? What should I do to get a integrable equation?

 

[haruspex]

The least confusing approach is to assign a variable T=T(t) to the tension and consider the two suspended masses separately.

 

[titansarus]

The least confusing approach is to assign a variable T=T(t) to the tension and consider the two suspended masses separately.

Now how to work with this T? I wrote $m_1 g - T = m_1 a$ and $T - m(t) g = m(t) a$ . Now maybe by dividing both sides, we get something like $m_1 g - T / (T - m(t) g) = m_1 / m(t)$ , we get an equation for T(t) in terms of $m_1$ and $m(t)$. It is $T(t) = 2 m_1 m(t) g / (m_1 + m(t))$ Also $m(t) = m_0 + \alpha t$ ($\alpha$ is negative).

Now I think I must write something like $m_0 dv/dt = (T - m(t) g) + v_0 \alpha~~~$ ? Is it OK? from this I get $m_0 dv = (T - (m_0 + \alpha t) g)~dt + v_0 \alpha ~ dt$
I used wolfram alpha to evaluate this and I get:
$\left(-\frac{2 g m_1^2 \log (\alpha t+m_0+m_1)}{\alpha}-\frac{1}{2} \alpha g t^2+\alpha v_0 t-m_0 g t+2 g m_1 t\right) = m_0 V(t)$ by assuming that $v$ of the system was at $t=0$ was zero. And we get $V(t)$ from here. Is it Right? Does it really get that complicated?

 

[haruspex]

Now I think I must write something like $m_0 dv/dt = (T - m(t) g) + v_0 \alpha~~~$ ?

No, you should have used that earlier:

Now how to work with this T? I wrote $m_1 g - T = m_1 a$ and $T - m(t) g = m(t) a$ .

v₀ features in the force balance on m₀.
When you have that right, your first step should be to eliminate T.

 

[titansarus]

No, you should have used that earlier:

v₀ features in the force balance on m₀.
When you have that right, your first step should be to eliminate T.

I think you mean something like: $m_0 dv / dt + (m_0 + \alpha t) g - v_0 \alpha = T$, right? Now should I substitute this in $T - m(t) g = m(t) a$ or maybe $m_1 g - T = m_1 a$? Or should I write something like $m_1 g - m(t) g = (m_1 + m(t)) a$? Or maybe both?

 

[titansarus]

No, you should have used that earlier:

v₀ features in the force balance on m₀.
When you have that right, your first step should be to eliminate T.

I evaluated what I said in post #5 (above post) and substituted T in the equation that has m(t) and multiplied them by $dt$ and I got a huge formula like: $\frac{2 \alpha^2 t {v_0}-4 g {m_1}^2 \log (\alpha t+{m_0}+{m_1})-g (\alpha t+{m_0}+{m_1})^2+6 g {m_1} (\alpha t+{m_0}+{m_1})}{2 \alpha} = m_0 v(t)$or actually this according to wolfram alpha:

If I substituted that in the equation with m1, it might get a little smaller but it will still be a big equation.

 

[haruspex]

I think you mean something like: $m_0 dv / dt + (m_0 + \alpha t) g - v_0 \alpha = T$, right?

A few problems there.
What is the mass on the left at time t?
Write the equation in the form ΣF=ma; that helps in getting the signs right.

 

[haruspex]

I got a huge formula like:

I also get a log function, but I don't think you should have had quadratic terms. Please post your working next time.