Auxiallry Field in a Coaxial Cable

[TFM]

Homework Statement

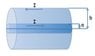
A coaxial cable consists of two very long cylindrical tubes, separated by linear insulating material of magnetic susceptibility χm (see Figure). A current I flows down the inner conductor and returns along the outer one, in each case the current distributes itself uniformly over the surface.

a)

Find the magnetic field in the region between the tubes.

b)

As a check, calculate the magnetization and the (surface and volume) bound currents. Confirm that (together with, of course, the free current) they generate the correct magnetic field.

Homework Equations

Just Section A at the moment:

I have a feeling that these equations are useful (hinted in a similar question in textbook)

$$\oint H .dl =I_{f_encl}$$

$$B = \mu H$$

$$\mu = \mu_0(1+\chi_m)$$

The Attempt at a Solution

$$B = \mu_0(1+\chi_m)H$$

Does this look okay, what could be a good thing to do next?

TFM

 

[Redbelly98]

You can use the integral expression you wrote to find H. Evaluate the integral around a circular loop.

Once you have H, your final expression can be used to get B.

 

[TFM]

So:

$$\oint H .dl =I_{f_encl}$$

I think I am doing the wrong integral, but would it be

$$H \pi^2 =I_{f_encl}$$

Or would this be for dA?

TFM

 

[Redbelly98]

No, not sure where you are getting pi^2 from.

The integral is evaluated going around the circumference of a circle.

 

[TFM]

I meant for that to be pi r squared, that's an area integral.

So would it be:

$$H 2 \pi r = I_{f_{encl}}$$

?

TFM

 

[Redbelly98]

Yes. So B = ?

 

[TFM]

So:

$$H 2 \pi r = I_{f_{encl}}$$

which rearranges to give H:

$$H = \frac{I_{f_{encl}}}{2\pi r}$$

and since:

$$B = \mu_0(1+\chi_m)H$$

B equals:

$$B = \mu_0(1+\chi_m)(\frac{I_{f_{encl}}}{2\pi r})$$

$$B = \mu_0(1+\chi_m)H$$

B equals:

$$B = \mu_0(1+\chi_m)(\frac{I_{f_{encl}}}{2\pi r})$$Does this look correct?

?

TFM

 

[Redbelly98]

Yes.

 

[TFM]

Excellent, thanks.

So for part B,

Question

As a check, calculate the magnetization and the (surface and volume) bound currents. Confirm that (together with, of course, the free current) they generate the correct magnetic field.

Useful Equations:

Magnetization Equation:

$$M = nm$$

Surface bound current Equation:

$$j_{ind} = M x \hat{S}$$

Volume bound Current Equation:

$$J_{ind} = \nabla x M$$

Edit These twi above equations should be curl, not x

I am not sure if these are the right equations to use, though?

Where would be the best place to start?

?

TFM

 

[TFM]

I have a feeling that this equation is very useful for the second part:

$$M = \chi_M H$$

where M is the Magnetization

Since we have worked out H to be:

$$H = \frac{I_{f_{encl}}}{2\pi r}$$

Is thuis a useful equation?

TFM

 

[TFM]

So for this question, would the equation for magnetization be:

$$M = \chi_M (\frac{I_{f_{encl}}}{2\pi r})$$

does this look right?

thus would the surface bound current be:

$$j_{ind} = \chi_M (\frac{I_{f_{encl}}}{2\pi r}) \times \hat{S}$$

And the Volume bound current:

$$J_{ind} = \nabla \times (\chi_M (\frac{I_{f_{encl}}}{2\pi r}))$$

Is this right? If so, what might be the next logical step?

?

TFM

 

[Redbelly98]

It has been a while since I worked on this stuff, so I don't know about part (b). Maybe somebody else can help out here?

 

[gabbagabbahey]

Hmmm... I think you'd better go back to part (a) for a moment, before I can help you through part (b) :

Let's make it a little more obvious which quantities are vectors and which are scalars; and what exactly you are integrating over...Ampere's Law for the Auxiliary Field $\vec{H}$ is:

[tex]\int_{\mathcal{P}} \vec{H} \cdot \vec{dl}=I_{f_{enc}}[/itex]<br /> <br /> Where $\mathcal{P}$ is an Amperian loop. While you seem to (thanks to RedBelly's assistance) have chosen the correct Amperian loop, you have neglected to explicitly state your choice and justify it's usefulness...<b>Hint:</b> How does the cylindrical symmetry in this problem help you here? Which direction must $\vec{H}$ point in?<br /> <br /> Once you have explicitly stated what your Amperian loop is, you should be able to explicitly determine the amount of free current enclosed in it, $I_{f_{enc}}$ in terms of the $I$ given in the problem.[/tex]

 

[TFM]

Where $${P}$$ is an Amperian loop. While you seem to (thanks to RedBelly's assistance) have chosen the correct Amperian loop, you have neglected to explicitly state your choice and justify it's usefulness...Hint: How does the cylindrical symmetry in this problem help you here? Which direction must $$\vec{H}$$ point in?

Well the Magnetic field will decrease in strength the further from the wire you get.

the $$\vec{H}$$ Should point in the direction of be radially outwards using right hand rule on diagram?

TFM

 

[gabbagabbahey]

No, $\vec{H}$ is not radially outwards...what are the free currents in this problem, and which direction do they point? Point your thumb in the direction of the current and your fingers will curl in the direction of the field...are you familiar with cylindrical coordinates $s$,$\phi$ and $z$? If you orient your coordinate system so that the axis of the cylinder is along the z-axis ($\hat{z}$ direction), then what direction does that give you for $\vec{H}$?

 

[TFM]

The free current is the current traveling in the wire. it is going upwards in the inner wire, and downwards in the outer cylinder/cable

I am slightly confused by:

Point your thumb in the direction of the current and your fingers will curl in the direction of the current

If your thumb points in the direction of the current, how can the curl of your fingers also be the current?

TFM

 

[gabbagabbahey]

Sorry, that was a typo; the second "current" was supposed to be "field"...I've edited my post.

...In terms of the cylindrical unit vectors, $\hat{s}$,$\hat{\phi}$ and $\hat{z}$, which direction do the currents flow (Don't worry about whether they flow in the positive or negative direction)?

 

[TFM]

Judging by this the field is flowing in circles, so in terms of cylindrical coordinates, it must be:

$$\hat{\phi}$$

TFM

 

[gabbagabbahey]

Yes, now what is the direction of $\vec{dl}$ If you choose a coaxial circle as your Amperian loop?

 

[TFM]

Would it be:

$$\hat{s}$$

Since it is for a circle of radius r through a full 360 degrees?

TFM

 

[gabbagabbahey]

If it were $\hat{s}$, then that would mean that as you went around the loop, for a small change in the magnitude $|\vec{dl}|$ , $s$ (or $r$ as you have it written) would change by an amount $|\vec{dl}|$ (Since that change would be in the $\hat{s}$ direction)...Does that sound right for a circle of constant radius $s$?

 

[TFM]

No it doesn't, it must be:

$$\hat{\phi}$$

TFM

 

[gabbagabbahey]

Yes, Good! ...so what is the dot product $\vec{H} \cdot \vec{dl}$?

 

[TFM]

Would it be

$$H\hat{\phi}$$

?

TFM

 

[gabbagabbahey]

Well, $$\vec{H}=H\hat{\phi}$$ and $$\vec{dl}=dl\hat{\phi}$$, so $$\vec{H} \cdot \vec{dl}=Hdl (\hat{\phi} \cdot \hat{\phi})$$

What is the dot product of the unit vectors $$\hat{\phi} \cdot \hat{\phi}$$?

 

[TFM]

Would that be 1?

?

TFM

 

[gabbagabbahey]

Yes, since after all; they are unit vectors...What does that make $\vec{H} \cdot \vec{dl}$?

 

[TFM]

Since:

$$\vec{H}=H\hat{\phi}$$

and

$$\vec{dl}=dl\hat{\phi}$$

Would that make

$$\vec{H} \cdot \vec{dl}$$

1?

TFM

 

[gabbagabbahey]

Nope,

$$\vec{H} \cdot \vec{dl}=Hdl (\hat{\phi} \cdot \hat{\phi})=Hdl *(1)=Hdl$$

Now what about the magnitude of $|\vec{dl}|=dl$...what is that for the circle? (remember, the only quantity that changes along the path is $\phi$)

 

[TFM]

Would this be:

$$\hat{s}$$

Since the magnitude will decrease the further out you get from the current?

TFM