Average of prime factors growth

[diegzumillo]

TL;DR

Average of number of prime factors have a curious fit, and I don't know what it means.

Hi there, bored physicist here. I wondered about factorization so I made some plots and a model fit to satiate my curiosity, but it only made me more curious. Now I just want the answers! I didn't know which prefix to use. "Hobbyist" seemed more appropriate but we don't have that so I went with "I" (undergrad level). Hope that works.

So I started calculating how many prime factors a number has, then plotted this number for all the numbers up to some arbitrary high number (I went up to a million). The plot was not very informative. (this one has 10000, for higher numbers the plot becomes an unreadable series of lines)

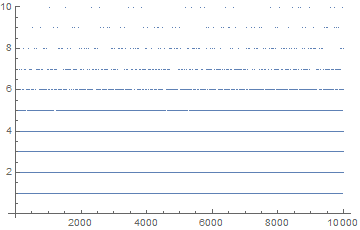
This looks like a random function. But, obviously we will start seeing higher number of factors the higher the number, so maybe if I take the average of the number of factors every batch of numbers that will tell me something interesting. So I experimented with different batch sizes (steps) to see if that influenced the result much, and it doesn't. It just narrows the curve a little, which is nice.

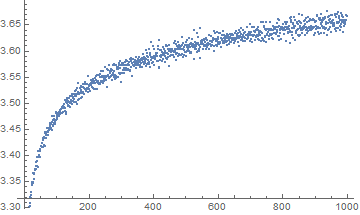
Bigger step/batch:

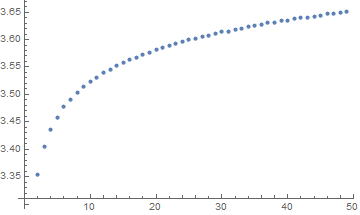
Naturally I wanted to know what curve this is, so I tried some naive fits. It looks like a square root of x so I tried a x^b. Close but definitely not it. Tried log, also close but not it. Then I went to wikipedia and, even though most of those number theory articles flew over my head, I did notice a recurrence of log(log(x)), so I tried that and got 1.27568 log ( log (815024. x - 600100.))

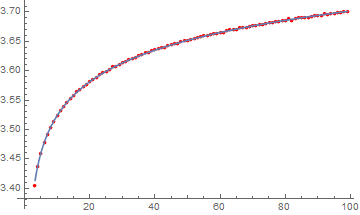
All right! that looks spot on!

but why? What are these numbers? Changing the step makes no difference on this fit, by the way.

 

[Keith_McClary]

This proves something using the Prime Number Theorem.

 

[mfb]

If you average over a sufficiently large range for sufficiently large numbers, a number n has a 1/(log(n)+1) chance to be prime, and a 1/n chance to be a divisor of a larger N. This makes our expected number of unique prime factors
$$\sum_{i=2}^{N} \frac{1}{n(\log(n)+1)} \approx \int_{x=2}^{N} \frac{1}{x(\log(x)+1)} =
\left[ \log(\log(x)+1)\right]_2^N = \log(\log N+1) + c $$ neglecting some edge effects.

 

[diegzumillo]

Nice! The expression is definitely recognizable. The differences come from counting all factors, not just the unique prime factors.
Do you have any more theorems in that hat of yours that could include multiplicities as well?

 

[mfb]

If we count primes with their powers, then a prime n will contribute 1/n + 1/n² + ... = 1/(n-1)

$$\int_{x=2}^{N} \frac{1}{(x-1)(\log(x)+1)} = \int_{x=1}^{N-1} \frac{1}{(x)(\log(x+1)+1)} \approx \int_{x=1}^{N} \frac{1}{x(\log(x)+1)} = \log(\log N+1) + c' $$
Same result just with a different constant*. You get an additional 1/2 from 2 (1/4 chance to have a second power of 2, 1/8 to have a third, ...), you increase the contribution from 3 from 1/3 to 1/2, but after that the changes get small quickly as higher prime powers are very rare.

*that constant is distorted by the sum to integral approximation and the primes being not evenly distributed, so it doesn't help to evaluate the integral for an estimate. You can take the sum for the first 1000 (or whatever) primes and use the integral from there on to get a better estimate of the constant.

 

[diegzumillo]

That's unexpected. I got some really specific numbers in there and I can't find a good fit with just that integration constant. I wonder if that fit I got only works for that range I used.

 

[mfb]

What is the range you simulate?

 

[diegzumillo]

(I had a gif of Mike Myers saying "ONE MILLION DOLLARS" but it was causing problems to post it here.)
Anyway, a million.
I know, I know, in the realm of number theory this must be laughably small.

 

[mfb]

log(log(N)+1)+1.005 looks spot-on if I take the bin centers and ignore the first few bins where the numbers vary significantly within the bins.

I use log for the natural logarithm here, if you don't use that then you need some additional factors.

Edit: Did some spot checks up to 10 million and there are some deviations, but the deviations are still below 0.2%.
Edit2: Reaching 0.23% deviation at 100 million. It's not perfect, but it's pretty close throughout. And that's a constant that I chose based on the first million. It's probably better to choose a constant based on the larger values.

Slightly broken formatting, but here are my numbers:

N	prime factors	logs	logs+c	diff	ratio
995000	3.7022	2.69533625473261	3.70033625473261	-0.001863745267388	0.999496584391068
3005000	3.7738	2.76731158045996	3.77231158045996	-0.001488419540043	0.999605591303184
5005000	3.8079	2.79886227781825	3.80386227781825	-0.004037722181753	0.998939645951377
7005000	3.8283	2.81912245793061	3.8241224579306	-0.004177542069395	0.998908773588957
10005000	3.8509	2.84016533031566	3.84516533031566	-0.005734669684338	0.998510823525841
20005000	3.8908	2.87984391188412	3.88484391188412	-0.005956088115885	0.998469186769846
30005000	3.9141	2.90234833992804	3.90734833992804	-0.00675166007196	0.998275041498184
40005000	3.9288	2.91801475659254	3.92301475659254	-0.005785243407455	0.998527478261185
50005000	3.9432	2.93000016348676	3.93500016348676	-0.008199836513243	0.997920512144136
60005000	3.9534	2.939687627776	3.944687627776	-0.008712372224002	0.997796233059138
70005000	3.9622	2.94780579067127	3.95280579067127	-0.00939420932873	0.997629042115812
80005000	3.9704	2.95478525510842	3.95978525510842	-0.01061474489158	0.997326530099844
90005000	3.974	2.96090145139401	3.96590145139401	-0.008098548605987	0.997962116606445
100005000	3.9804	2.96634109051274	3.97134109051274	-0.009058909487262	0.997724120820203
N	prime factors	logs	logs+c	diff	ratio

And here is the python code that produced the second column:

import math

def primefactors(num,f=0):
    if num<4:
        return f+1
    for i in range(2,int(math.sqrt(num))+1):
        if num%i == 0:
            return f+1+primefactors(num/i)
    return f+1

for k in range(4000,10001,1000):
    sum=0.
    for i in range(10000*k,10000*(k+1)):
        sum+=primefactors(i)
    print(sum/10000)

 

[mfb]

Look what I got with a bit more curve-fitting: log(log(N)+0.57)+1.036
From the range 60000-70000 to the range 100 million to 100 million+10000 (using bins of 10000 to 1 million, and then the numbers from above) the maximal deviation is 0.0023, or 0.06%.
In the 500 million bin the real number is 4.0614 and the approximation is 4.06130. That's corresponding to an error of just 1 prime factor in 10,000 numbers.

Why 0.57? I don't know. Maybe a better estimate for the prime density somehow. Could also be some other approximation I made.

 

[suremarc]

Why 0.57? I don't know. Maybe a better estimate for the prime density somehow. Could also be some other approximation I made.

Just a wild guess, but the Euler-Mascheroni constant is around ~0.577 and it appears in asymptotic formulas for some number theoretical functions.

 

[diegzumillo]

Sigh. Sometimes I hate my ADD-riddled brain. I'm staring at your code, then at my code, then at my plot, then at your data, and I could not understand why we were getting different results. In my laziness I did the fit without using the actual numbers, but their indices instead! since I was using steps of 1000 or even bigger, the fit was trying to work with 1,2,3,4... instead of the center of the bin, 1000, 2000,... or whatever the number of steps.

But I'm on the same page now! I have very similar numbers :D

This was pretty fun.

 

[mfb]

Small improvement in the prime density. $\pi(x) = \frac x {\log x}$, therefore $\pi'(x) = \frac {\log x-1} {\log^2 x} = \frac{1}{\log x} - \frac{1}{\log^2 x}$.
Compare this to $\frac{1}{\log (x) + 1} = \frac{1}{\log x} - \frac{1}{\log^2 x} + \frac{1}{\log^3 x} \pm ...$ which has extra terms.

The new expression leads to an integral of log(log(x))+1/log(x)+c using the same shift trick and approximation as before.
That fits worse than the empirical function before, however. log(log(x)-0.44)+1/log(x)+1.036 leads to a great fit again.