B Field of Large Ring Magnet Calculation

[jok]

Hi Everyone ,

Can anyone explain why I am getting negative result with a large Neodymium N35 ring Magnet ?

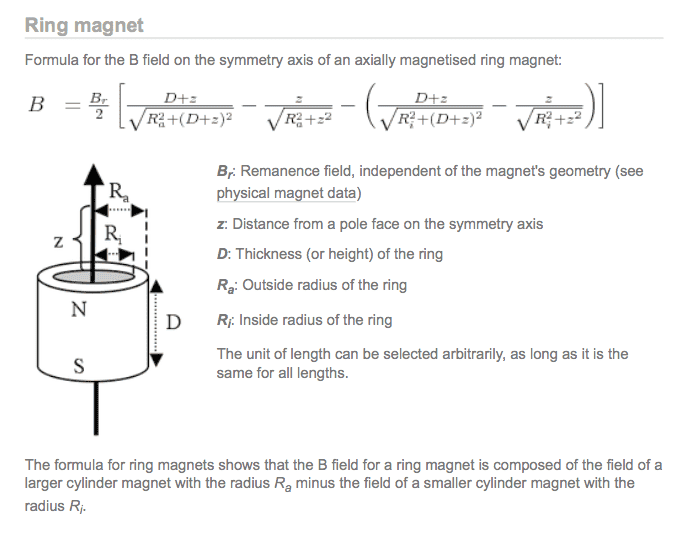
Br: Remanence field, independent of the magnet's geometry
z: Distance from a pole face on the symmetry axis
D: Thickness (or height) of the ring
Ra: Outside radius of the ring
Ri: Inside radius of the ring

Br: 12,300
z: 5mm
D: 10mm
Ra: 360mm
Ri: 330mm

(12000÷2)×((10+5)÷(SQRT((POWER(360,2)+POWER((10+5),2))))−(5)÷(SQRT((POWER(360,2)+POWER((5),2))))−((10+5)÷(SQRT((POWER(330,2)+POWER((10+5),2))))−(5)÷(SQRT((POWER(330,2)+POWER((5),2))))))

I am getting a result of : -15.0893364057539 Gauss .

Does it make sense for such a large magnet ?

Thank you

 

[berkeman]

Welcome to the PF.

I'd suggest doing it with a calculator and writing down the value of each term individually. Then see if you can spot the error in your (Excel?) formula calculation above.

 

[jok]

Welcome to the PF.

I'd suggest doing it with a calculator and writing down the value of each term individually. Then see if you can spot the error in your (Excel?) formula calculation above.

I did.

The results are correct .

Some said it is due to the fact that in the center of the ring there is very little field flux, which make sense . The center Z axis is very much away from the actual magnet.

So far what I came up with is using a block magnet formula to calculate a ring magnet by converting it to liner from circular .

But if there is a function for surface ring magnet strength. it would be very helpful.

Thank you

 

[Bri1]

Hi, how did you get your value for z? I'm new to this and trying to work a similar problem, any help would be much appreciated