Balancing a plank on a cylinder

[simon janssens]

Homework Statement

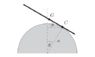
The figure shows a uniform thin rigid plank of length 2b which can roll
without slipping on top of a rough circular log of radius a. The plank is initially
in equilibrium, resting symmetrically on top of the log, when it is slightly
disturbed. Find the period of small oscillations of the plank.

2. Additional context
The wording of the question implicates that we can use sinϑ ≈ ϑ and cosϑ ≈ 1 because ϑ² ≈ 0.
The plank has no thickness and the mass is uniformly distributed.
Gravity is constant.

The Attempt at a Solution

I figured that the resulting force is always pointed perpendicular to the plank in the center of mass. This results in a torque τ = r × F_⊥ .
r = |GC| = ϑa because there is no slipping
|F_⊥| = mgcosϑ = mg (rounding for small angles)
so the torque is τ = mgaϑ

Then I try calculating the moment of inertia of the plank, I use the formula for parallel axes of rotation so that the moment of inertia is I = I_CM + mh²
I_CM = ml²/12 = mb²/3
mh² = m|GC|² = ma²ϑ² = 0
so the moment of inertia is I = mb²/3

This gives me enough to calculate the angular acceleration, ϑ'' = τ/I = 3ga/b² ⋅ ϑ
I deduce that ϑ is directly proportional with its second derivative.
ϑ has to be of the form e^λt or Asin(ωt +φ₀).
Because I'm looking for an oscillation, my guess is that it will be of the latter.
Now I have 3 variables and 3 equations, at t = 0 we get :
ϑ(0) = ϑ₀ = Asin(ω⋅0 +φ₀)
ϑ'(0) = 0 = ωAcos(ω⋅0 +φ₀)
ϑ''(0) = 3ga/b² ⋅ ϑ₀ = -ω²Asin(ω⋅0 +φ₀)

I tried solving these, but it didn't work, can you help me please ?
Thanks a lot,
S.

 

[haruspex]

This gives me enough to calculate the angular acceleration, ϑ'' = τ/I = 3ga/b² ⋅ ϑ
.

When θ is positive, will its acceleration be positive or negative?

 

[simon janssens]

When θ is positive, will its acceleration be positive or negative?

It should be negative, because the plank is always accelerating towards the point of equilibrium. So should it be ϑ''(0) = -3ga/b² ⋅ ϑ ?
I probably made a mistake with the vector product τ = r × F_⊥

 

[simon janssens]

UPDATE ----
thanks to haruspex I noticed that i calculated τ = r × F_⊥ incorrectly, when taking clockwise as positive, the torque should be negative.
This makes the angular acceleration opposed to ϑ, as expected.
this gives 3 equations and 3 variables, as before :
ϑ(0) = ϑ₀ = Asin(φ₀)
ϑ'(0) = 0 = ωAcos(φ₀)
ϑ''(0) = -3ga/b2 ⋅ ϑ₀ = -ω²Asin(φ₀) = -ω²ϑ₀

this solves to
φ₀ = π/2
A = ϑ₀
ω = 1/b ⋅√(3ga/ϑ₀)
the period of this function is T = 2πb√(ϑ₀/(3ga))

is this correct ? can someone check please ?

 

[haruspex]

ω = 1/b ⋅√(3ga/ϑ₀)

I would not expect ω to depend on the amplitude. Please check your working.