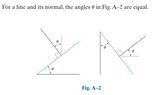
Discussion Overview
The discussion revolves around the concept of angles in the context of statics, particularly focusing on the relationship between normal lines and other angles in geometric configurations. Participants express confusion regarding the introduction of these concepts in their textbooks and seek clarification on the geometric principles involved.
Discussion Character
- Exploratory
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants express confusion about how angles are defined in their textbooks, particularly regarding the normal line and its relationship to other angles.
- One participant references a geometric theorem about perpendicular lines being equal, suggesting a connection to the discussion.
- Another participant discusses the importance of normal forces in the context of friction and how these forces relate to the orientation of surfaces.
- A later reply introduces a mathematical framework using vectors to describe forces acting on a particle in a rotated coordinate system, emphasizing the normal force's role.
- Some participants suggest using geometry to identify missing angles in the triangles formed by intersecting lines.
- There is a mention of interpreting angles in relation to horizontal and vertical orientations, indicating differing perspectives on the geometric relationships involved.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus, as multiple interpretations and approaches to understanding the angle concepts are presented. There is ongoing confusion and debate regarding the definitions and relationships of the angles discussed.
Contextual Notes
Some participants note the absence of transversal angles in their understanding, and there is uncertainty regarding the assumptions made in the textbook's presentation of the concepts. The discussion includes various interpretations of geometric relationships without resolving these differences.