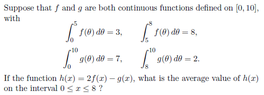Basic definite integral question

[TheFallen018]

Hey, I've got this problem I've been doing, but I'm not sure if my approach is right. My textbook has pretty much less than a paragraph on this sort of stuff.

View attachment 8444

My thinking was that since an integral is a sum, in order to get the range from 0 to 8, we should just be able to add or subtract the definite integrals as required. eg. $\int_{0}^{5}f(\Theta )d\Theta + \int_{5}^{8}f(\Theta)d\Theta = \int_{0}^{8}f(\Theta)d\Theta = 3+8=11$

So, following this line of thinking, I found $\int_{0}^{8}h(x)dx$ to be $2*11-5=17$. Then, by dividing by 8, we should get the average value of $h(x)$ to be ($\frac{17}{8}$).

It feels like I'm missing something though. Does this look right? Thanks

 

[Ackbach]

Yes, you would need to do this:
\begin{align*}
\langle h\rangle&=\frac18\int_0^8h(x)\,dx \\
&=\frac18\int_0^8(2f(x)-g(x))\,dx \\
&=\frac18\left[2\int_0^8f(x)\,dx-\int_0^8g(x)\,dx\right] \\
&=\frac18\left[2\left(\int_0^5f(x)\,dx+\int_5^8f(x)\,dx\right)-\left(\int_0^{10}g(x)\,dx-\int_8^{10}g(x)\,dx\right)\right].
\end{align*}
Then you can plug in what you know. Note: the $\langle h\rangle$ notation means "the average value of $h$."