- #1
- 927
- 484
Summer is coming and brings a new basic math challenge! Enjoy! For more advanced problems you can check our other intermediate level math challenge thread!
RULES:
1) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
2) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
3) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
4) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
5) Mentors, advisors and homework helpers are kindly requested not to post solutions, not even in spoiler tags, for the challenge problems, until 16th of each month. This gives the opportunity to other people including but not limited to students to feel more comfortable in dealing with / solving the challenge problems. In case of an inadvertent posting of a solution the post will be deleted by @fresh_42##1.## (resolved in post #62) a) Prove ##(e+x)^{e-x}>(e-x)^{e+x}## for ##0<x<e.##
##\space## ##\space## b) Show that for ##0 < b < a## we have
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\dfrac{1}{a} < \dfrac{2}{a+b} < \dfrac{\log (a) - \log (b)}{a-b} < \dfrac{1}{\sqrt{ab}} < \dfrac{1}{b}##
##\space## ##\space## c) Let ##f,g\, : \,[a,b]\longrightarrow \mathbb{R}## be two monotone integrable functions, either both increasing or both decrasing. ##\space## ##\space## ##\space## ##\space## ##\space## Show that
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space####\space## ##\space## ##\int_a^bf(x)g(x)\,dx \ge \int_a^bf(x)\,dx \cdot \int_a^bg(x)\,dx## ##\space## ##\space## (by @fresh_42)
##2.## (solved by @PeroK ) One card out of a deck has been lost. The other 51 cards are repeatedly shuffled and then thirteen cards are dealt, face up. The cards are 2 spades, 3 clubs, 4 hearts, and 4 diamonds. What is the chance that the missing card is (a) spade, (b) club, (c) heart, (d)diamond ##\space## ##\space## (by @StoneTemplePython)
##3.## (solved by @lpetrich ) Farmer Joe bought the blue area for $10,000, the green for $20,000 and the yellow for $30,000. Assuming prices are proportional to the areas, what's the price for his entire field?
Figure:
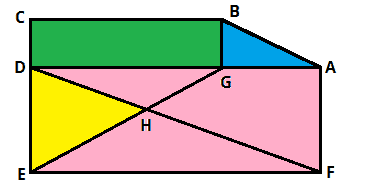
(by @fresh_42)
##4.## (solved by @Phylosopher ) Using only geometric reasoning, calculate the average value of ##f(x) = \sqrt{2x - x^2}## on ##
[0,2]##
(by @QuantumQuest)
##5.## (resolved in post #64) Can one pack 53 bricks, each of dimension ##\text{1 x 1 x 4}## into a ##\text{6 x 6 x 6}## box?
(by @StoneTemplePython)
##6.## (solved by @fishturtle1 ) Show that ##a^{13} - a \equiv 0(\mod 2730)## for all ##a \in \mathbb{Z}## ##\space## ##\space## (by @QuantumQuest)
##7.## (solved by @lpetrich ) The general solution to ##y^{(4)}(x)+4y(x)=0## is given by
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##y(x)=\alpha e^{-x}\cos (x) + \beta e^{-x}\sin (x) + \gamma e^x \sin (x) + \delta e^x \cos (x)##
a) How do we have to choose the initial conditions at ##x=0## in order to get ##y(x)=e^{-x}\cos x## as unique solution?
b) Which function do we get for the initial conditions
##y'(0)=1 \; , \;y''(0)=0\; , \; y'''(0)=0\; , \; y^{(4)}(0)=0\,## ? ##\space## ##\space## (by @fresh_42)
##8.## (resolved in post #63) Find the points where the graphs of ##f(x) = e^{-x}## and ##g(x) = e^{-x}\cos x## are tangent to each other. Find another function whose graph is tangent to the graphs of the aforementioned functions in one of the contact points ##\space## ##\space## (by @QuantumQuest)
##9.## (solved by @lpetrich ) Decode:
a) ZC ULX QFFY L TBXCFSB FMFS XZYVF ZC RLX AZXVDMFSFA TDSF CULY KZKCB BFLSX LPD, LYA LOO PDDA CUFDSFCZVLO IUBXZVZXCX IHC CUZX YHTQFS HI DY CUFZS RLOO LYA RDSSB LQDHC ZC
b) CO PXLIX BPX Y FPRDMCPO MP KPDOM, Y BDRR LIXCAYMCPO PX VXPPB SDFM ZI WCAIO. YOFJIXF JCMU OP VXPPB JCRR ZI CWOPXIL. CM CF BCOI MP DFI OPOMXCACYR XIFDRMF JCMUPDM VXPPB YF RPOW YF EPD KCMI MUIS YOL YF RPOW YF CM CF KPSSPO QOPJRILWI MP YRR SYMUISYMCKCYOF. JUIMUIX MUI RYMMIX CF FYMCFBCIL JCRR ZI LIKCLIL PO Y KYFIZEKYFI ZYFCF. CB EPD UYAI FIIO MUI VXPZRIS ZIBPXI YOL XISISZIX MUI FPRDMCPO, EPD KYOOPM VYXMCKCVYMI CO MUI FPRDMCPO MP MUYM VXPZRIS ##\space## ##\space## (by @fresh_42)
##10.## (solved by @Mr Davis 97 ) Calculate
$$ \int_{\pi^{-1}}^\pi \dfrac{1}{x}\sin^2 \left( -x-\dfrac{1}{x} \right) \log x\,dx $$ (by @fresh_42)
RULES:
1) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored.
2) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
3) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
4) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
5) Mentors, advisors and homework helpers are kindly requested not to post solutions, not even in spoiler tags, for the challenge problems, until 16th of each month. This gives the opportunity to other people including but not limited to students to feel more comfortable in dealing with / solving the challenge problems. In case of an inadvertent posting of a solution the post will be deleted by @fresh_42##1.## (resolved in post #62) a) Prove ##(e+x)^{e-x}>(e-x)^{e+x}## for ##0<x<e.##
##\space## ##\space## b) Show that for ##0 < b < a## we have
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\dfrac{1}{a} < \dfrac{2}{a+b} < \dfrac{\log (a) - \log (b)}{a-b} < \dfrac{1}{\sqrt{ab}} < \dfrac{1}{b}##
##\space## ##\space## c) Let ##f,g\, : \,[a,b]\longrightarrow \mathbb{R}## be two monotone integrable functions, either both increasing or both decrasing. ##\space## ##\space## ##\space## ##\space## ##\space## Show that
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space####\space## ##\space## ##\int_a^bf(x)g(x)\,dx \ge \int_a^bf(x)\,dx \cdot \int_a^bg(x)\,dx## ##\space## ##\space## (by @fresh_42)
##2.## (solved by @PeroK ) One card out of a deck has been lost. The other 51 cards are repeatedly shuffled and then thirteen cards are dealt, face up. The cards are 2 spades, 3 clubs, 4 hearts, and 4 diamonds. What is the chance that the missing card is (a) spade, (b) club, (c) heart, (d)diamond ##\space## ##\space## (by @StoneTemplePython)
##3.## (solved by @lpetrich ) Farmer Joe bought the blue area for $10,000, the green for $20,000 and the yellow for $30,000. Assuming prices are proportional to the areas, what's the price for his entire field?
Figure:
(by @fresh_42)
##4.## (solved by @Phylosopher ) Using only geometric reasoning, calculate the average value of ##f(x) = \sqrt{2x - x^2}## on ##
[0,2]##
(by @QuantumQuest)
##5.## (resolved in post #64) Can one pack 53 bricks, each of dimension ##\text{1 x 1 x 4}## into a ##\text{6 x 6 x 6}## box?
(by @StoneTemplePython)
##6.## (solved by @fishturtle1 ) Show that ##a^{13} - a \equiv 0(\mod 2730)## for all ##a \in \mathbb{Z}## ##\space## ##\space## (by @QuantumQuest)
##7.## (solved by @lpetrich ) The general solution to ##y^{(4)}(x)+4y(x)=0## is given by
##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##\space## ##y(x)=\alpha e^{-x}\cos (x) + \beta e^{-x}\sin (x) + \gamma e^x \sin (x) + \delta e^x \cos (x)##
a) How do we have to choose the initial conditions at ##x=0## in order to get ##y(x)=e^{-x}\cos x## as unique solution?
b) Which function do we get for the initial conditions
##y'(0)=1 \; , \;y''(0)=0\; , \; y'''(0)=0\; , \; y^{(4)}(0)=0\,## ? ##\space## ##\space## (by @fresh_42)
##8.## (resolved in post #63) Find the points where the graphs of ##f(x) = e^{-x}## and ##g(x) = e^{-x}\cos x## are tangent to each other. Find another function whose graph is tangent to the graphs of the aforementioned functions in one of the contact points ##\space## ##\space## (by @QuantumQuest)
##9.## (solved by @lpetrich ) Decode:
a) ZC ULX QFFY L TBXCFSB FMFS XZYVF ZC RLX AZXVDMFSFA TDSF CULY KZKCB BFLSX LPD, LYA LOO PDDA CUFDSFCZVLO IUBXZVZXCX IHC CUZX YHTQFS HI DY CUFZS RLOO LYA RDSSB LQDHC ZC
b) CO PXLIX BPX Y FPRDMCPO MP KPDOM, Y BDRR LIXCAYMCPO PX VXPPB SDFM ZI WCAIO. YOFJIXF JCMU OP VXPPB JCRR ZI CWOPXIL. CM CF BCOI MP DFI OPOMXCACYR XIFDRMF JCMUPDM VXPPB YF RPOW YF EPD KCMI MUIS YOL YF RPOW YF CM CF KPSSPO QOPJRILWI MP YRR SYMUISYMCKCYOF. JUIMUIX MUI RYMMIX CF FYMCFBCIL JCRR ZI LIKCLIL PO Y KYFIZEKYFI ZYFCF. CB EPD UYAI FIIO MUI VXPZRIS ZIBPXI YOL XISISZIX MUI FPRDMCPO, EPD KYOOPM VYXMCKCVYMI CO MUI FPRDMCPO MP MUYM VXPZRIS ##\space## ##\space## (by @fresh_42)
##10.## (solved by @Mr Davis 97 ) Calculate
$$ \int_{\pi^{-1}}^\pi \dfrac{1}{x}\sin^2 \left( -x-\dfrac{1}{x} \right) \log x\,dx $$ (by @fresh_42)
Attachments
Last edited by a moderator:
