- #1
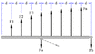
Bending moment diagram for overhanging beam
- Thread starter David Lewis
- Start date
Click For Summary
SUMMARY
The discussion focuses on constructing a bending moment diagram for an overhanging beam, specifically an airplane wing spar subjected to a distributed load represented as a semi-ellipse. The participants emphasize the importance of identifying the nature of the load: if the upward force components (F1...Fn) are equal, they can be simplified to a Uniformly Distributed Load (UDL); if they vary, they should be treated as a Variable Distributed Load (VDL). The formula for calculating the bending moment is highlighted as F1 * d + F2 * 2d, where 'd' represents the distance from the point of interest.
PREREQUISITES- Understanding of free-body diagrams
- Knowledge of bending moment calculations
- Familiarity with distributed loads, specifically UDL and VDL
- Basic principles of structural mechanics
- Study the principles of bending moment diagrams in structural analysis
- Learn about Uniformly Distributed Loads (UDL) and Variable Distributed Loads (VDL)
- Explore the application of semi-elliptical load distributions in engineering
- Review case studies on bending moment calculations for overhanging beams
Structural engineers, mechanical engineers, and students studying mechanics of materials who are involved in analyzing and designing beams under various loading conditions.
- #2
lingesh
- 28
- 2
If those upward force components F1...Fn are equal in magnitude,then you can simplify it as UDL. If they are different and varying gradually you can consider it as UVL and solve the problem.
- #3
David Lewis
- 847
- 259
Thanks for your reply. The spar sees a distributed load -- the load diagram is a semi-ellipse. I approximated the distributed load as point loads. I'd like to know the formula to calculate the bending moment, e.g. F1 * d + F2 * 2d...
- #4
