Bending shear stress distribution

[piygar]

I modeled a simple cantilever rectangular beam in Patran of (L,W,H = 100, 6, 4) with Hexa8 elements and applied a vertical shear load (upwards) of some magnitude at the free end.
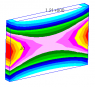
Ran in Nastran and plotted the vertical shear stress distribution on a cross-section in middle of length (in order to avoid any boundary condition effects). which is parabolic as expected being zero at top and bottom edges and maximum at center.
But shear stress distribution is not uniform across width. I was expecting rectangular bands parallel to horizontal edges but i get curved bands across widths. what could be the reason of that?
Have attached the fringe plot of vertical shear stress distribution.

 

[PhanthomJay]

The parabolic shear stress formula VQ/It assumes a uniform shear stress distribution along the width. The computer shows otherwise. What sort of a range of shear stresses do you get along the width at say the neutral axis? How do the values compare to the hand calculation?

 

[piygar]

Shear stress at neutral axis along the width varies from 5.15 at the center to 8.07 at the either end of the width.
Have inserted fringe plot with spectrum.
I applied 100 unit shear load at the cantilever tip so according to formula max shear stress at center should be 1.5* 100/(6*4) = 6.25

 

[PhanthomJay]

Shear stress at neutral axis along the width varies from 5.15 at the center to 8.07 at the either end of the width.
Have inserted fringe plot with spectrum.
I applied 100 unit shear load at the cantilever tip so according to formula max shear stress at center should be 1.5* 100/(6*4) = 6.25

View attachment 98605

Thanks for the data. Funny things happen at edges and corners and when beams are not narrow. Anyway, the 6.25 seems like a good weighted average. With the addition of a good catch-all safety factor, of course! Unless the cantilever is of short length, shear doesn't add much in comparison to bending stresses, and I've always ignored it in long cantilever designs using steel.

 

[piygar]

Thanks for reply. Wanted to understand the corners/edges effect clearly.
Also plotted the horizontal shear stress (due to vertical shear load!) on the same cross-section and got this.

Horizontal shear is small but not numeric zero.
Discussed with a colleague and suspicion pointed to Poisson's ratio. Ran another simulation with Poisson ratio = zero and voila, Vertical shear stress is constant across width, and zero horizontal shear stress due to vertical shear load.
Since width of beam is not small,came to understanding that cross-section behaving like a plane strain condition instead of plane stress.
Though plane strain condition should produce secondary normal stress, not shear stress.

 

[PhanthomJay]

When you set Poisson's ratio equal to 0 and got uniform stress distribution across the width, how did the result compare to the VQ/It shear stress 6.25 value at the neutral axis?

 

[piygar]

It comes 6.12 at the neutral axis with zero Poisson ratio.
(Tried with higher order Hexa, Hexa20 elements and got same result, as i had shear locking effect in mind)

 

[PhanthomJay]

Thanks for info!