hdp12
- 67
- 2
Summary:: Hello there, I'm a mechanical engineer pursuing my graduate degree and I'm taking a class on machine learning. Coding is a skill of mine, but statistics is not... anyway, I have a homework problem on Bernoulli and Bayesian probabilities. I believe I've done the first few parts correctly, but the final question asks me to explain why one is more accurate than another, and the inverse as well. I am not sure, so I figured I'd reach out here and ask. The work and appropriate equations are below:
1. (10 pts) Consider 20 values randomly sampled from the Bernoulli Distribution with parameter :
(a) Estimate the parameter using the maximum likelihood approach and the 20 data values.
(b) Estimate the parameter using the Bayesian approach. Use the beta distribution Beta(a=8, b=4).
(c) Estimate the parameter using the Bayesian approach. Use the beta distribution Beta(a=4, b=8).
(d) Discuss why the estimation from (b) is more accurate than that from (a) and why the estimation from (c) is worse than that from (a).
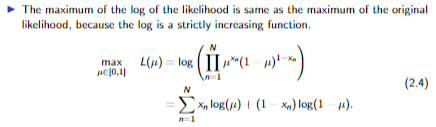

Thanks in advance for any help!
1. (10 pts) Consider 20 values randomly sampled from the Bernoulli Distribution with parameter :
Matlab:
x = [1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1];
N = length(x);(a) Estimate the parameter using the maximum likelihood approach and the 20 data values.
Matlab:
u = sum(x==1)/N; % u = 0.75
bern = (u.^x).*(1-u).^(1-x)
p = 0;
for n = 1:N
pTemp = x(n)*log(u) + (1-x(n))*log(1-u);
p = p+pTemp;
end
%ln(a) = b <--> a = e^b
p = exp(p); % p = 1.3050e-05
Matlab:
% a + sum(xn),b + N - sum(xn)
% (8 + 15 - 1) / (12 + 20 - 2) = 22/30
u = 22/30; % u = 0.7333(c) Estimate the parameter using the Bayesian approach. Use the beta distribution Beta(a=4, b=8).
Matlab:
% (4 + 15 - 1) / (12 + 20 - 2) = 18/30
u = 18/30; % u = 0.6
Matlab:
uA = 0.75;
uB = 0.7333;
uC = 0.6;Thanks in advance for any help!