Discussion Overview
The discussion revolves around the characterization of the singularity in a Schwarzschild black hole, specifically whether it is time-like or space-like as represented in a diagram. Participants analyze the implications of hyperbolas in different quadrants of the diagram and reference terminology used in a textbook, debating the accuracy of the descriptions provided.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
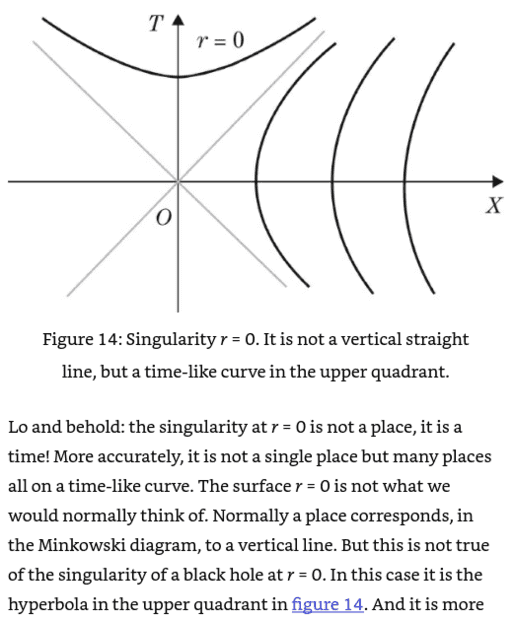
- Some participants assert that hyperbolas in the right quadrant are time-like and those in the upper quadrant are space-like, questioning the textbook's claim about the singularity being time-like.
- Others argue that the singularity in a Schwarzschild black hole is spacelike, suggesting that the book contains significant errors in its description.
- A participant references Wald's work to support their claim about the nature of the singularity, indicating a disagreement with the textbook's interpretation.
- There is a discussion about the correct interpretation of hypersurfaces, with some stating that a hypersurface is spacelike if the normal vectors are timelike, leading to confusion regarding the terminology used in the textbook.
- Several participants propose that the errors in the textbook may be due to typos or inconsistent terminology, with some suggesting that the author may be using terms in a non-standard way.
- Concerns are raised about the pedagogical implications of the author's terminology and whether it aligns with standard conventions in the literature.
Areas of Agreement / Disagreement
Participants do not reach a consensus, as there are multiple competing views regarding the characterization of the singularity and the accuracy of the textbook's terminology. Disagreements persist about whether the issues stem from typos or a misunderstanding of standard terminology.
Contextual Notes
Participants note that the definitions of time-like and space-like can depend on the metric signature convention adopted, which adds complexity to the discussion. The conversation highlights the potential for confusion in the context of general relativity and the interpretation of hypersurfaces.