Block on a Plane Ex from Morin-Statics

[veezbo]

Homework Statement

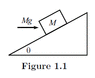
Example (Block on a plane): A block of mass M rests on a fixed plane inclined
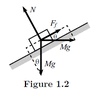
at angle theta. You apply a horizontal force of Mg on the block, as shown in figure 1-1 (attached). The free-body diagram for this is also attached as an image.

Assume that the friction force between the block and the plane is large enough
to keep the block at rest. What are the normal and friction forces (call them N
and F_f) that the plane exerts on the block?

Homework Equations

Just the use of basic statics?
Also trigonometric expressions involving sin and cos

The Attempt at a Solution

I initially try to find F_f itself by drawing the vector connection the heads of F_f and the Mg applied force (as shown in the free-body diagram).
However, I cannot find F_f this way.
I think there is something I am missing while trying to balance the forces.

 

[hikaru1221]

Write down the vector equation for forces in equilibrium $$\Sigma \vec{F} = 0$$, and solve it

 

[veezbo]

Thanks Hikaru! I had never actually heard of statics before, and my book (Morin) was not very clear on how this worked.

But I think I finally figured out how it works.

I have another question though: since F_f = Mg * sin(theta) - Mg * cos(theta), shouldn't this imply that the magnitude of F_f is that same expression?
If so, then I feel like there should also be a geometric solution.

 

[hikaru1221]

I also agree that Morin's book isn't so instructive and therefore not appropriate at introductory level, though insightful. It requires the readers to know quite a lot before reading it.

Yes, you got the correct answer This lies behind one equation: $$\Sigma \vec{F} = 0$$, which can be viewed under either geometric angle or algebraic approach.