Discussion Overview
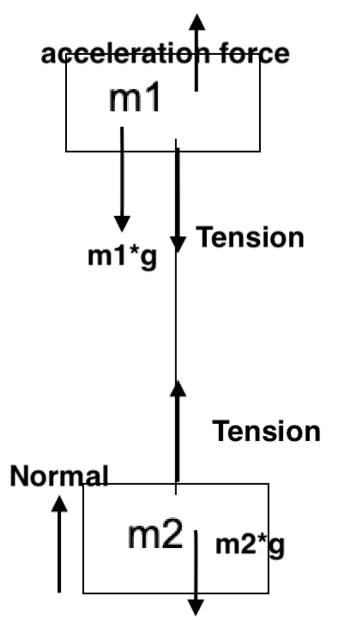
The discussion revolves around the dynamics of two blocks, m1 and m2, connected by a string, where m1 is shot upward with an initial velocity while m2 remains stationary. Participants explore the forces acting on m1, particularly the tension in the string and the implications of various assumptions about the system's behavior.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants propose that if block m2 is not lifted, the tension T does not exceed m2g.
- Others argue that when the string is loose, there is no tension, and m1 moves solely under the influence of gravity until the string becomes taut.
- A participant suggests that the tension could reach a maximum value when m1 reaches the end of the string, but this depends on various factors such as initial velocity and string properties.
- Some contributions discuss modeling the string as a spring, leading to equations involving tension and acceleration, but there is uncertainty about the conditions under which these models apply.
- There is a debate about whether m1 can have zero acceleration while still being tethered, with some asserting that it cannot instantaneously stop without infinite tension.
- Participants mention the impulse-momentum theorem and the need for a functional relationship for tension to avoid infinitely many solutions.
- Clarifications are made regarding whether the connection is modeled as a string or a spring, with implications for the physical behavior of the system.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the behavior of the system, particularly concerning the nature of tension, the conditions for acceleration, and the modeling of the string. The discussion remains unresolved with no consensus reached.
Contextual Notes
Limitations include the dependence on initial conditions, the assumptions made about the string's properties, and the unresolved nature of the equations governing the system's dynamics.