adamaero
- 109
- 1
An exciton is a bound electron-hole pair (in a semiconductor). For this problem, think of an exciton as a hydrogen-like atom, with a negatively charged electron and positively charged hole orbiting each other.
The permittivity of free space (ε0) is replaced with permittivity of the semiconductor (ε = 12).
The mass of the electron is replaced with the effective mass of the electron-hole pair.
1. Homework Statement (bold below is what I really need help on)
A) Estimate the radius in nm and the ground state energy in eV for an exciton in Si.
B) Approximately how large is the separation between atoms in a crystal of silicon? How does the radius compare with this number?
C) Silicon atoms have an average kinetic energy of T*kB. How does the exciton binding energy (E1) compare with this number? What does this mean?
D) All this is about electrostatic potential energy. Prove that it's reasonable to neglect the gravitational potential energy.
me = 9.1*10-31
eV = 1.602×10−19 J (N*m)
h = 6.626*10-34
ħ = 1.055*10-34
a0 = 0.0529 nm
ε*ε0 = 1.0359*10-10
permittivity of silicon = εSi = kSiε0 where k = dielectric constant
effective masses
me* = 0.26me
mh* = 0.36me
r = mek2e4/(πħ3)
me*mh*/(me* + mh*) = 0.15me
r = n2h2*1.0359*10-10/(z*π*meffectivee2)
A)
12*a0/0.15 = 4.2nm (n2/z)
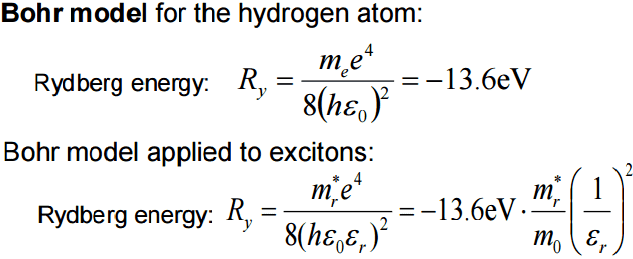
Ry = -13.6eV
B) I do not remember chemistry much. How is the separation between silicon atoms found?
C) 300*1.38*10-23 m2kg/s2 = 4.14*10-23
E1 = ?
D) PEelectrostatic = kqQ/r
images.slideplayer.com/22/6421287/slides/slide_3.jpg
FE = qE
Fg = mg
∴ qE = mg
& as long as qE/m is much larger than g, gravity can be ignored.
Sources
http://www.course-notes.org/book/export/html/10891
https://upload.wikimedia.org/wikipedia/commons/9/97/Exciton_energy_levels.jpg
The permittivity of free space (ε0) is replaced with permittivity of the semiconductor (ε = 12).
The mass of the electron is replaced with the effective mass of the electron-hole pair.
1. Homework Statement (bold below is what I really need help on)
A) Estimate the radius in nm and the ground state energy in eV for an exciton in Si.
B) Approximately how large is the separation between atoms in a crystal of silicon? How does the radius compare with this number?
C) Silicon atoms have an average kinetic energy of T*kB. How does the exciton binding energy (E1) compare with this number? What does this mean?
D) All this is about electrostatic potential energy. Prove that it's reasonable to neglect the gravitational potential energy.
me = 9.1*10-31
eV = 1.602×10−19 J (N*m)
h = 6.626*10-34
ħ = 1.055*10-34
a0 = 0.0529 nm
ε*ε0 = 1.0359*10-10
permittivity of silicon = εSi = kSiε0 where k = dielectric constant
effective masses
me* = 0.26me
mh* = 0.36me
Homework Equations
r = mek2e4/(πħ3)
me*mh*/(me* + mh*) = 0.15me
r = n2h2*1.0359*10-10/(z*π*meffectivee2)
The Attempt at a Solution
A)
12*a0/0.15 = 4.2nm (n2/z)
Ry = -13.6eV
B) I do not remember chemistry much. How is the separation between silicon atoms found?
C) 300*1.38*10-23 m2kg/s2 = 4.14*10-23
E1 = ?
D) PEelectrostatic = kqQ/r
images.slideplayer.com/22/6421287/slides/slide_3.jpg
FE = qE
Fg = mg
∴ qE = mg
& as long as qE/m is much larger than g, gravity can be ignored.
Sources
http://www.course-notes.org/book/export/html/10891
https://upload.wikimedia.org/wikipedia/commons/9/97/Exciton_energy_levels.jpg