Hello Bordiba,
a) I say we keep things as simple as possible. For our first function, let's try an absolute value function whose axis of symmetry is at $$x=\frac{1}{2}$$, and has the required roots and area. So let's begin with:
$$f(x)=A|2x-1|+B$$
With the required roots in mind, we may write:
$$f(0)=f(1)=A+B=0\,\therefore\,A=-B$$
With the required triangular area in mind, we find:
$$\frac{1}{2}(1-0)B=1\,\therefore\,B=2$$
and so we have:
$$f(x)=-2|2x-1|+2$$
Here is a plot of the function:
View attachment 1124
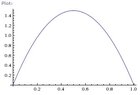
Next, let's try a quadratic function.
With the required roots in mind, we may write it as:
$$f(x)=Ax(x-1)=A\left(x^2-x \right)$$
With the required area in mind, we may write:
$$A\int_0^1 x^2-x\,dx=1$$
Applying the FTOC, we have:
$$A\left[\frac{1}{3}x^3-\frac{1}{2}x^2 \right]_0^1=1$$
$$A\left[2x^3-3x^2 \right]_0^1=6$$
$$A\left(2-3 \right)=6$$
$$A=-6$$
And so we have:
$$f(x)=6x(1-x)$$
Here is a plot of the function:
View attachment 1125
b) To find the arc-lengths, we need only apply the Pythagorean theorem for the first function:
$$s=2\sqrt{\left(\frac{1}{2} \right)^2+2^2}=\sqrt{17}$$
For the second function, we will use:
$$s=2\int_0^{\frac{1}{2}}\sqrt{1+(6(1-2x))^2}\,dx$$
Using the trigonometric substitution:
$$6(1-2x)=6-12x=\tan(\theta)\,\therefore\,-12\,dx=\sec^2(\theta)\,d\theta$$
we have:
$$s=\frac{1}{6}\int_0^{\tan^{-1}(6)}\sec^3(\theta)\,d\theta$$
With a bit of manipulation, we can get this in a form we can integrate directly:
$$\sec^3(\theta)=\frac{1}{2}\left(\sec^3(\theta)+ \sec^3(\theta) \right)=\frac{1}{2}\left(\sec^3(\theta)+ \sec(\theta)\left(\tan^2(\theta)+1 \right) \right)=$$
$$\frac{1}{2}\left(\sec^3(\theta)+ \sec(\theta)\tan^2(\theta)+\sec(\theta)\frac{\tan(\theta)+ \sec(\theta)}{\tan(\theta)+\sec(\theta)} \right)=$$
$$\frac{1}{2}\left(\left(\sec(\theta)\sec^2(\theta)+\sec(\theta)\tan^2(\theta) \right)+\left(\frac{\sec(\theta)\tan(\theta)+\sec^2(\theta)}{\sec(\theta)+\tan(\theta)} \right) \right)=$$
$$\frac{1}{2}\frac{d}{d\theta}\left(\sec(\theta)\tan(\theta)+\ln\left|\sec(\theta)+\tan(\theta) \right| \right)$$
So now we have:
$$s=\frac{1}{12}\int_0^{\tan^{-1}(6)}\,d \left(\sec( \theta)\tan( \theta)+\ln\left|\sec( \theta)+\tan( \theta) \right| \right)$$
Applying the FTOC, we have:
$$s=\frac{1}{12}\left[\sec( \theta)\tan( \theta)+\ln\left|\sec( \theta)+\tan( \theta) \right| \right]_0^{\tan^{-1}(6)}=$$
$$\frac{1}{12}\left(6\sqrt{37}+\ln\left(\sqrt{37}+6 \right) \right)\approx3.249029586202852$$
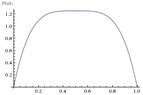
c) Let's try a quartic function this time, since the area seem to be decreasing as the order increases. We may try:
$$f(x)=A\left(x-\frac{1}{2} \right)^4+B$$
With the root requirements in mind, we find:
$$f(0)=f(1)=\frac{A}{16}+B=0\,\therefore\,A=-16B$$
Now, with the requirement on the area in mind, we may write:
$$B\int_0^1 1-16\left(x-\frac{1}{2} \right)^4\,dx=1$$
Applying the FTOC, we have:
$$B\left[x-\frac{16}{5}\left(x-\frac{1}{2} \right)^5 \right]_0^1=1$$
$$B\left[5x-16\left(x-\frac{1}{2} \right)^5 \right]_0^1=5$$
$$B\left(\left(5-\frac{1}{2} \right)-\left(0+\frac{1}{2} \right) \right)=5$$
$$B=\frac{5}{4}$$
Thus, our function is:
$$f(x)=-20\left(x-\frac{1}{2} \right)^4+\frac{5}{4}=\frac{5}{4}\left(1-(2x-1)^4 \right)$$
Here is a plot of the function:
View attachment 1126
Using numeric integration, we find the arc-length is:
$$s=\int_0^1\sqrt{1+100(2x-1)^6}\,dx\approx
2.96314204075918$$