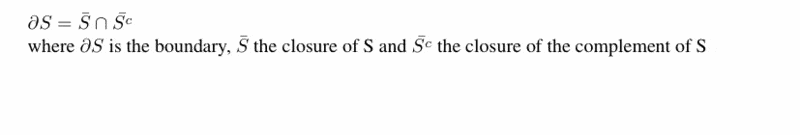SUMMARY
The boundary of a set S is defined as the intersection of the closure of S and the closure of the complement of S. This relationship is crucial in topology and requires a clear understanding of the definitions of "closure" and "boundary" as they can vary across different mathematical domains. The discussion emphasizes the importance of using precise definitions to derive this relationship effectively. Participants are encouraged to clarify these definitions to facilitate accurate problem-solving.
PREREQUISITES
- Understanding of topological concepts such as "closure" and "boundary".
- Familiarity with set theory and its operations.
- Knowledge of the complement of a set in a topological space.
- Basic skills in mathematical proof techniques.
NEXT STEPS
- Research the definitions of "closure" and "boundary" in various mathematical contexts.
- Study the properties of topological spaces and their implications for set operations.
- Explore examples of boundary and closure in metric spaces.
- Learn about the relationship between interior, closure, and boundary in topology.
USEFUL FOR
Mathematics students, particularly those studying topology, set theory, or advanced calculus, will benefit from this discussion. It is also useful for educators seeking to clarify these concepts for their students.