Build an expression for the remaining area & show that....

[mathlearn]

Data

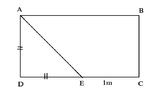
From the rectangular glass sheet ABCD the isosceles triangular part ADE is cut away (See figure)

The length of CE is 1m.

View attachment 5978

Problem

i. Take the length of DE as x meters, write an expression in terms of x , for the area of the remaining part of the sheet.

The area of the remaining part ABCE is $5cm^2$

ii.Show that $x^2+2x-10=0$ Workings:

Area of the remaining part = area of the rectangle - area of the isosceles triangle = $ [(x+1) x ]- \frac{1}{2} x^2 = x^2 + x- \frac{1}{2} x^2 $

Where do I need help

I think my expression for the remaining area is correct but how can i show that it is
$x^2+2x-10=0$ when the area of the remaining part is $5cm^2$

 

[MarkFL]

Let's first treat $ABCE$ as a trapezoid, hence:

$$A=\frac{h}{2}(B+b)=\frac{x}{2}((x+1)+1)=\frac{x}{2}(x+2)$$

Now, let's treat is as a rectangle less the right isosceles triangle:

$$A=x(x+1)-\frac{1}{2}x^2=\frac{x}{2}(2x+2-x)=\frac{x}{2}(x+2)$$

Now, if we equate this area to 5 (assuming all measures are in cm), we obtain:

$$\frac{x}{2}(x+2)=5$$

Multiply through by 2:

$$x(x+2)=10$$

Distribute on the left:

$$x^2+2x=10$$

Subtract through by 10:

$$x^2+2x-10=0$$