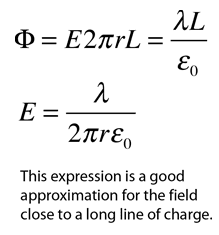SUMMARY
The discussion centers on the application of Gauss' law to determine the electric field, specifically questioning whether the formula p/(π*ε*r^2) is valid. Participants reference Schaum's Electromagnetics (4th ed) by Edminister and a HyperPhysics resource for clarification. Key points include the importance of calculating flux correctly, considering both the end caps and lateral area of the closed surface, and the necessity of using the correct surface area formula for a cylinder, which is 2πrL, not πr²L. The consensus is that the first method is dimensionally incorrect.
PREREQUISITES
- Understanding of Gauss' law in electromagnetism
- Familiarity with electric flux calculations
- Knowledge of surface area formulas for geometric shapes
- Basic principles of radial electric fields
NEXT STEPS
- Study the derivation and applications of Gauss' law in electromagnetism
- Learn how to calculate electric flux through various surfaces
- Review the geometry of cylinders and their surface area calculations
- Explore the implications of dimensional analysis in physics equations
USEFUL FOR
Physics students, educators, and anyone interested in mastering electromagnetism and the application of Gauss' law in electric field calculations.