Calculate double integral of the intersection of the ellipse and circle

[zs96742]

how to calculate the double integral of f(x,y) within the intersected area?

f(x,y)=a₀+a₁y+a₂x+a₃xy

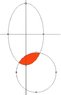
The area is the intersection of an ellipse and a circle.

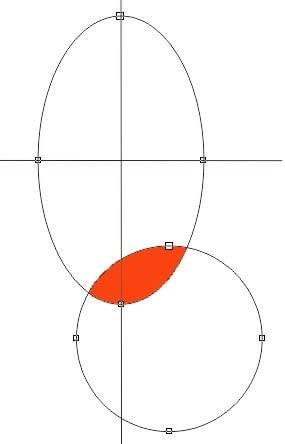
Any help will be appreciated, I don't know how to do this.

can I use x=racosθ,y=rbsinθ to transformer the ellipse and circle?
If I can, what's the equation for the circle?
what's the range for r while calculating.

 

[HallsofIvy]

Well, it's your circle! I don't see how anyone else can tell you what its equation is. The equation of a circle with center at (x_0, y_0) and radius r is, of course, (x- x_0)^2+ (y- y_0)^2= r^2. How to integrate depends on exactly how the two figures overlap. x= r cos(\theta), y= r sin(\theta) assumes that r is measured from (0, 0). That might be useful if you were to "translate" your system so that the center of the circle is at the origin.

 

[zs96742]

Well, it's your circle! I don't see how anyone else can tell you what its equation is. The equation of a circle with center at (x_0, y_0) and radius r is, of course, (x- x_0)^2+ (y- y_0)^2= r^2. How to integrate depends on exactly how the two figures overlap. x= r cos(\theta), y= r sin(\theta) assumes that r is measured from (0, 0). That might be useful if you were to "translate" your system so that the center of the circle is at the origin.

Yes, I forgot this, the center of the circle and the ellipse, the radius, the a and b are all known. That means I can calculate the intersection points.

If you chose the circle center as the origin, what's the equation for the ellipse?

 

[mathman]

From the picture and your previous remark, I suggest the following.

Get the x values of the intersection points - outer integral in x.

Use the y = for the ellipse as the lower and the y = for the circle as the upper limit - inner integral in y.
Since y is defined as a square root for both figures, make sure you pick the correct sign.

 

[zs96742]

From the picture and your previous remark, I suggest the following.

Get the x values of the intersection points - outer integral in x.

Use the y = for the ellipse as the lower and the y = for the circle as the upper limit - inner integral in y.
Since y is defined as a square root for both figures, make sure you pick the correct sign.

In this case, I have to separate the area, any chance I can use polar coordinate?

 

[mathman]

In this case, I have to separate the area, any chance I can use polar coordinate?

What is the need to separate? It seems to me polar coordinates make it more complicated.

I also realized later, the y integral is trivial, since the integrand is 1. All you need to do is write the x integrand as the difference between the equation for y of the circle piece minus the equation for the ellipse piece.