Calculate polarization energy over a set of cuboids

Click For Summary

Discussion Overview

The discussion revolves around calculating the polarization energy of a system composed of orthogonal cuboids with varying dielectric properties. The central cuboid contains a charge distribution and has a dielectric constant of vacuum, while surrounding cuboids have homogeneous but anisotropic dielectric constants. Participants explore methods for deriving the polarization energy equation and consider the feasibility of analytical versus numerical solutions.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant describes the configuration of cuboids and the specific charge distribution within the central cuboid, seeking assistance in formulating the polarization energy equation.
  • Another participant suggests that the problem may only be solvable numerically, noting the rarity of analytical solutions for such systems.
  • A different participant acknowledges the numerical approach but emphasizes the importance of efficiency in the chosen method, as it can significantly affect the solution's convergence to an analytical result.
  • One participant proposes that finite element methods might be the most suitable for addressing the problem.

Areas of Agreement / Disagreement

Participants express differing views on the solvability of the problem, with some suggesting numerical methods while others acknowledge the potential for analytical solutions in specific cases. The discussion remains unresolved regarding the best approach to take.

Contextual Notes

Participants have not reached a consensus on the method for calculating polarization energy, and there are uncertainties regarding the efficiency and effectiveness of various numerical techniques versus analytical solutions.

Who May Find This Useful

This discussion may be of interest to researchers and students in electrostatics, computational physics, and materials science, particularly those dealing with dielectric materials and numerical modeling techniques.

Glxblt76
Messages
7
Reaction score
1
Dear Physics Forums members,

I have a research problem that involves electrostatics. My education is as a chemist, and thus I struggle to accurately represent my problem, so I thought that you guys could help me (and would be interested in the exercise).

Here is an image to summarize my problem.
PnBTzPq.png

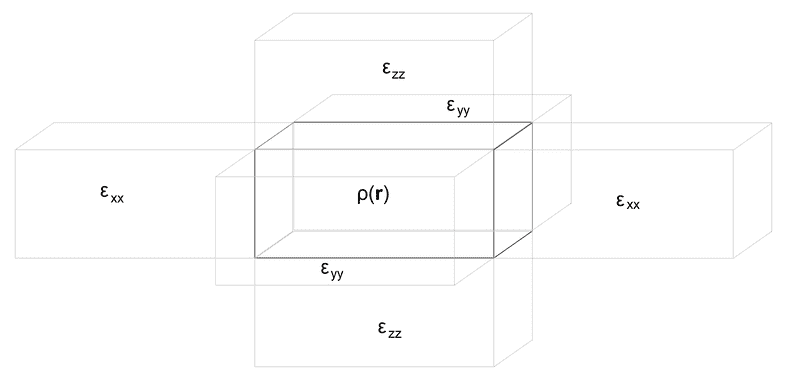
So, in the starting point of my problem, I have my space divided into orthogonal cuboids. The cuboid at the center is particular: there is a charge distribution within it, ρ(r) and its dielectric constant is that of vacuum. All other orthogonal cuboids contain homogeneous, but not isotropic, continua. In the x direction, the dielectric constant is εxx, the component of the dielectric constant tensor ε, in y direction it is εyy, and in z direction it is εzz.
I explicitely represent three cuboids around the central cuboid in each direction, for a total of 73 - 1 = 342 cuboids. This big cuboid is immersed into a continuum that corresponds to the average value of the dielectric constant tensor ε.

What I would like to write is the equation for the polarization energy of this system (i. e. the energy change caused by replacing a conventional cuboid by a cuboid containing the charge distribution ρ(r) and with the dielectric constant of vacuum).
The system is electrostatic, i e there is no variation of the magnetic field with time. It obeys the two equations:
∇E = ρ/ε0
∇×E = 0

I know the dimension of the cuboid (the 3 lengths a, b and c from which the cuboid can be reconstructed).

I'm a bit lost and I don't know where to start.
Do some people have suggestions?

All the best!
 

Attachments

  • PnBTzPq.png
    PnBTzPq.png
    3.9 KB · Views: 475
Last edited:
Science news on Phys.org
Do not hesitate to ask questions if this does not sound clear to you!
 
I fear the problem is only solvable numerically. There are very few systems for which it is possible to obtain analytical solutions of the resulting polarisation.
 
I know it, but my question is about how can I do it efficiently, because depending on the method you choose, your solution may be reached slower or faster to the point it's practically indistinguishable from an analytical solution.
 
I suppose finite element methods are most adequate.
 
  • Like
Likes   Reactions: Glxblt76
Thanks. I will think about it.
 

Similar threads

Graduate Investigating the dielectric constant of a pure polar liquid
  • · Replies 0 ·
Replies
0
Views
2K
Graduate Polarization charge density of homogeneous dielectric
  • · Replies 3 ·
Replies
3
Views
4K
Graduate Numerical solution of the Poisson equation
  • · Replies 3 ·
Replies
3
Views
1K
Undergrad How Do Dielectrics Influence Electric Flux Density in Electromagnetic Theory?
  • · Replies 5 ·
Replies
5
Views
2K
Graduate Electric and magnetic field lines in a plane wave of finite extent
  • · Replies 1 ·
Replies
1
Views
2K
How Do You Calculate the Electrostatic Energy of a Hollow Conducting Sphere?
  • · Replies 5 ·
Replies
5
Views
2K
The height of a dielectric material between two coaxial pipes
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Work to move a point charge from infinity to the centre of a charge distribution
  • · Replies 4 ·
Replies
4
Views
2K
Electrostatic Energy in the Hydrogen Atom
  • · Replies 4 ·
Replies
4
Views
4K
Graduate What is Gauss' Law for Dielectrics and How Does it Account for Polarization?
  • · Replies 5 ·
Replies
5
Views
6K