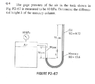
Calculate Pressure from Height & Specific Gravity
Click For Summary
The discussion focuses on calculating pressure using specific gravity and height in a fluid context. Participants clarify that the density of a liquid can be derived from the density of water multiplied by its specific gravity. The gauge pressure is emphasized as the difference between actual pressure and atmospheric pressure, allowing participants to ignore atmospheric pressure in their calculations. A key point is the need to equate the sum of pressure contributions to the given gauge pressure of 80 KPa. Ultimately, the correct height calculation is confirmed to be approximately 0.582 meters, despite initial confusion over the calculations.
Similar threads
- · Replies 10 ·
- · Replies 7 ·
- · Replies 13 ·
- · Replies 4 ·