SUMMARY
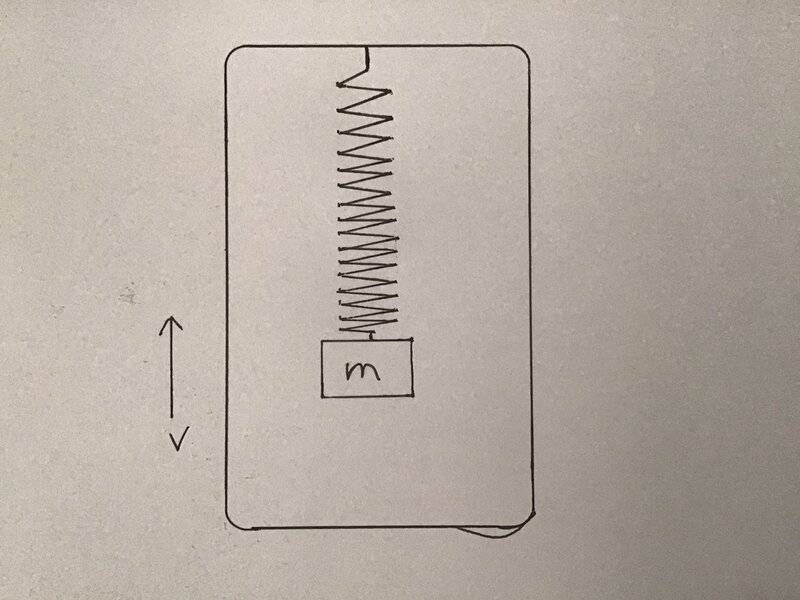
The discussion focuses on calculating the net energy of a system involving a mass and a Slinky in an elevator. The Slinky is designed to fully contract in 1 second, during which the mass is weightless and moves upward at a constant speed of 1 m/s. The key equations presented include E(initial) = 1/2mv^2 + E(slinky stretch) + E(mass linky x g x height slinky) and E(final) = (1/2mv^2 + mgh) + E(kinetic energy from slinky stretch) + E(kinetic energy from slinky height). The conclusion drawn is that the difference between final and initial energy equals the potential energy gained by the mass, expressed as E(final) - E(initial) = mgh.
PREREQUISITES
- Understanding of classical mechanics principles, particularly energy conservation.
- Familiarity with potential and kinetic energy concepts.
- Knowledge of the behavior of elastic materials, specifically Slinky dynamics.
- Basic grasp of motion in non-inertial reference frames, such as elevators.
NEXT STEPS
- Study the principles of energy conservation in mechanical systems.
- Learn about the dynamics of elastic materials, focusing on Slinky behavior.
- Explore the effects of non-inertial reference frames on perceived motion.
- Examine detailed examples of potential and kinetic energy calculations in similar systems.
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in understanding energy dynamics in systems involving elastic materials and non-inertial frames.
 Am I missing something?
Am I missing something?