TGV320
- 40
- 26
- Homework Statement
- Help in order to solve a determinant
- Relevant Equations
- Determinants
Hello,
I need some advice because I just can't figure out how to solve the problem. I could try to make the determinant triangular by adding all the b together, but that doen't seem a good way of solving the problem. Is there any direction I should be thinking of?
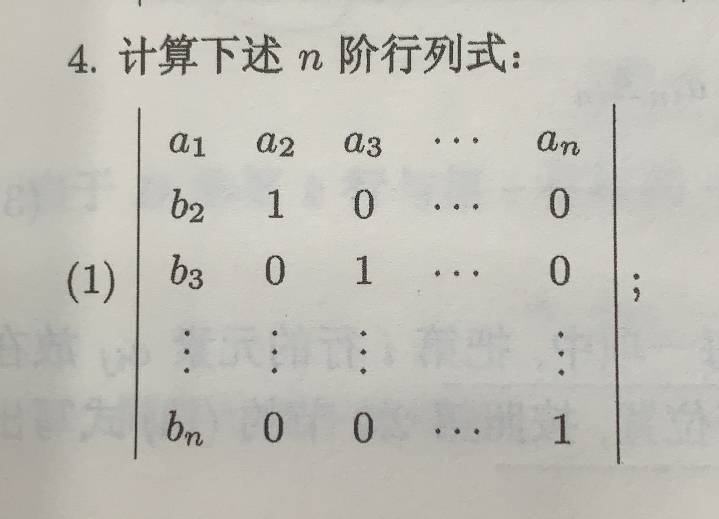 Thanks
Thanks
I need some advice because I just can't figure out how to solve the problem. I could try to make the determinant triangular by adding all the b together, but that doen't seem a good way of solving the problem. Is there any direction I should be thinking of?