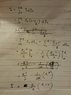Calculating Current in a Cylindrical Region

[Aviegaille]

Homework Statement

(a)The current density across a cylindrical region of radius R varies according to the equation: J=J0(1-r/R), where r is the distance from the axis of the cylinder. The current density is the maximum J0 at the axis r=0 and decreases linearly to zero at the surface r=R. Calculate the current in terms J0 and the region's cross sectional area A=pi*R^2.

(b) Now suppose that a current density was a maximum Jo at the surface and decreased linearly to zero at the axis, so that: J=J0 r/R. Calculate the current. Why is the result different for these two cases?

Homework Equations

I=JA

The Attempt at a Solution

I uploaded a picture of the first part but I am not sure if it's correct. I also don't know how to get the area from this problem. I am thinking of plugging the value of R from I to get the area but I am pretty sure it is not right.

 

[Simon Bridge]

You cannot just use the total cross-section because the current density is different in different parts of the cylinder.
Instead you have to add up the contributions from each small part of the area.
i.e. you need to set up an integral.

If I is the current and J is the current density, then dI = J.dA

 

[Aviegaille]

You cannot just use the total cross-section because the current density is different in different parts of the cylinder.
Instead you have to add up the contributions from each small part of the area.
i.e. you need to set up an integral.

If I is the current and J is the current density, then dI = J.dA

Can you elaborate how can I use that equation?

 

[Simon Bridge]

You integrate both sides.
You need an expression for J in terms of r and an expression for dA in terms of dr.
Hint: how much current passes through the area between r and r+dr?