A cart with two cylindrical wheels connected by a rod

[physics_CD]

Homework Statement

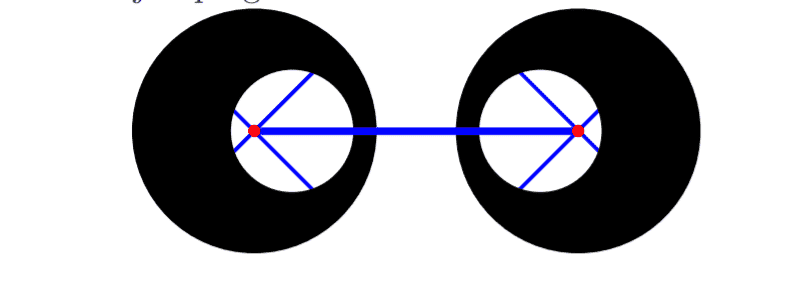
A cart has two cylindrical wheels connected by a weightless horizontal rod using weightless spokes and frictionless axis as shown in the figure. Each of the wheels is made of a homogeneous disc of radius R, and has a cylidrical hole of radius R/2 drilled coaxially at the distance R/3 from the centre of the wheel. The wheels are turned so that the holes point towards each other, and the cart is put into motion on a horizontal floor. What is the critical speed v by which the
wheels start jumping?

Relevant Equations

.

Firstly I only consider one of the wheels. This wheel consists of a big wheel (black) with mass M and radius R and inside it a circular region with a negative mass (-m) and radius R/2. (I assume they have same mass density but with opposite signs. I do this because I don't know where the center of mass is - By doing this the region with both negative and positve mass becomes the drilled cylindrical hole). Now the wheel is rotating and I choose to use a rotating frame of reference by adding the centrifugal force $m \omega^2 \frac{R}{3}=m \frac{3 v^2}{R}$ for the cylindrical hole at a distance R/3 from the center of the wheel. This force must be pointing at the center of the wheel since it has a "negative mass", and therefore do the opposite of what normal mass would do. There is also a gravitational force given by $mg$. This force is poiting upward since the mass is negative. I would assume that the critical speed happens when the net force in the y-direction is no longer 0 for one of the wheels. The net force in the y-direction for the hole system consisting of 2 wheels is still 0. Before the critical speed I would assume that the vertical component of $m \frac{3 v^2}{R}$ equals $mg$. But I have difficulty writing up an equation for both wheels and how they push or pull each other (if they even do so). Do I even need to consider the second wheel since this problem is symmetrical? Can I say that the critical speed happens when the cylindral hole starts to "slip" (of course this can't happen i reality. But I just pretend it can and say $\mu$ between the cylindral hole and the wheels equals 1) Can someone help?

The correct answer is $v=3 \sqrt {gR}$

 

[haruspex]

The centrifugal force acts on the hole, but gravity acts on the whole.

 

[hutchphd]

The friction isn't really the issue...each wheel will start to "hop" vertically. Does the fact that they are connected matter?

 

[haruspex]

The friction isn't really the issue...each wheel will start to "hop" vertically. Does the fact that they are connected matter?

Yes, I think you have to assume the frictional coefficient is large enough that slipping does not occur. Otherwise the wheels could rotate at different rates.
That its two connected wheels in this arrangement is to ensure the speed is constant.

 

[hutchphd]

Now the wheel is rotating and I choose to use a rotating frame of reference by adding the centrifugal force...

Yes. But what is the rotational speed of the center of the "hole" (it is not v...)??

 

[kuruman]

That its two connected wheels in this arrangement is to ensure the speed is constant.

Did you really mean to say that the speed is constant as opposed to "the same for both wheels"? I am imagining that the speed of this contraption increases from zero until the center of each wheel reaches the critical speed.

 

[haruspex]

Did you really mean to say that the speed is constant as opposed to "the same for both wheels"? I am imagining that the speed of this contraption increases from zero until the center of each wheel reaches the critical speed.

Not sure that it makes any difference, but you could just as easily read the question as the cart's being set into motion at a given speed and asking at what threshold speed it would undergo hopping. Or the speed is very gradually increased until it hops. Since no acceleration is given, we must assume either that it is irrelevant or so low that it is effectively constant speed as hopping commences.

 

[physics_CD]

Yes. But what is the rotational speed of the center of the "hole" (it is not v...)??

thank you for pointing that out. The velocity at that point should be $\omega \frac{R}{3}+v$ where v is the linear speed for the whole system.

 

[haruspex]

thank you for pointing that out. The velocity at that point should be $\omega \frac{R}{3}+v$ where v is the linear speed for the whole system.

I think @hutchphd is suggesting you reconsider the relationship between the linear velocity of the cart and the angular velocity of the hole's centre.