Calculating current with and without internal resistance

[ddobre]

Homework Statement

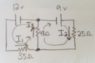
Calculate the magnitudes and directions of the currents in each of the 3 resistors in the circuit above, if...
(a) ...both batteries have zero internal resistance.
(b) ...each battery has an internal resistance of 1.0 Ω.

Homework Equations

I1 = I2 + I3 (Node Law)

The Attempt at a Solution

I tried to use the node law to define the direction of the current, and for part a) I got I3 = .1452A,
I1 = .06398A, and I2 = .08122A. I'm not sure if this is correct but this is how I tried to solve part a). For part b), since the batteries now have internal resistance, I added two 1 ohm resistors to the circuit, on the left and right of the node at the top, (next to the negative terminals of the batteries). But, I had issues trying to solve the series of equations with 5 resistors in the circuit. I tried to solve for each anyway, but with poor results, (I couldn't narrow down one current). I would try to solve with an Req, but I need the current through each resistor. Any advice?

 

[Hesch]

I tried to use the node law to define the direction of the current

Don't use the node law to define directions. Just define. You are free to choose directions.

If your choise - as for an arrow direction - turns out to be opposite to the physical positive current direction, the resulting current will just be negative.

You can use the KVL law, as you have indicated, and you have two "windows" ( left and right ) that can be used as circular current paths.

If you choose the left and right current path to be counter clockwise, you will get the KVL equation for the left window:

12V - I_left*35Ω - I_left*48Ω + I_right*48Ω = 0

Now, write the equation as for the right window and calculate I_left and I_right.

I_left and I_right are virtual currents, not physical

The physical currents are calculated:

I1 = I_left
I3 = I_left - I_right
I2 = -I_right

You may alternatively use KCL to calculate node voltages, then use Ohms law to calculate currents.

 

[phinds]

But, I had issues trying to solve the series of equations with 5 resistors in the circuit. I tried to solve for each anyway, but with poor results, (I couldn't narrow down one current). I would try to solve with an Req, but I need the current through each resistor. Any advice?

So, will the current through the new resistors be different, in the new circuit, from the current through the exiting resistors that they are in series with. In other words, why are you worrying about 5 resistors when you only have 3?

 

[ddobre]

Don't use the node law to define directions. Just define. You are free to choose directions.

If your choise - as for an arrow direction - turns out to be opposite to the physical positive current direction, the resulting current will just be negative.

You can use the KVL law, as you have indicated, and you have two "windows" ( left and right ) that can be used as circular current paths.

If you choose the left and right current path to be counter clockwise, you will get the KVL equation for the left window:

12V - I_left*35Ω - I_left*48Ω + I_right*48Ω = 0

Now, write the equation as for the right window and calculate I_left and I_right.

I_left and I_right are virtual currents, not physical

The physical currents are calculated:

I1 = I_left
I3 = I_left - I_right
I2 = -I_right

You may alternatively use KCL to calculate node voltages, then use Ohms law to calculate currents.

Would the right loop be: 9V - 25I_right-48I_right+48I_left = 0

 

[ddobre]

So, will the current through the new resistors be different, in the new circuit, from the current through the exiting resistors that they are in series with. In other words, why are you worrying about 5 resistors when you only have 3?

No, current should remain the same since the resistors are in series with each other

 

[Hesch]

Would the right loop be: 9V - 25I_right-48I_right+48I_left = 0

If you choose the left and right current path to be counter clockwise,

You have chosen the right circular current path to be clockwise, and that's ok except +48I_left then becomes -48I_left.

The reason why you have to choose directions ( arrows ) before setting up equations, is that you must respect your chosen directions! Otherwise you will get a wrong result.

 

[Hesch]

No, current should remain the same since the resistors are in series with each other

Of course the currents through two resistors in series will be the same, but this common current will change, when an inner resistance in the battery is inserted.