- #1
ddobre
- 33
- 2
Homework Statement
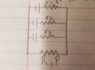
Three identical batteries are first connected in parallel to a resistor. The power dissipated by the resistor is measured to be P. After that, the batteries are connected to the same resistor in series and the dissipated power is measured to be 4P (four times larger than for the parallel connection). Find the internal resistance of each of the batteries if the resistor has resistance R.
Homework Equations
P = IV = I^2R = V^2/R
V = IR
(Parallel): 1/Req = 1/R1 + 1/R2
(Series): Req = R1 +R2
The Attempt at a Solution
With this problem, it is the fact that instead of resistors, I have batteries with resistances that confuses me. Nevertheless, I tried using the standard parallel resistor equation to solve for each of the individual internal resistances of the batteries. This is what I tried to do, knowing current would vary in parallel: P = I^2R, P = (I1)2 * r1. Then I would solve for r1. Similarly, I tried P = V^2/R to find the resistances of the series circuit: P = V2/r1. But I can't help thinking something is missing is wrong. I have a feeling that since I'm analyzing battery internal resistances, these equations won't work. Any advice?