Timisoarian
- 2
- 0
Hey all,
So I have this beam problem and I honestly am lost with it!
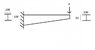
The beam is I-section cantilever, tapers in depth along its length (See picture attached) with a point load at the free end. I am trying to figure out the deflection formula and how to derive it! Also, when calculating its bending stress and shear stress, is it the same way as a normal beam?
Please guys, any help is appreciated it as I am completely lost!
So I have this beam problem and I honestly am lost with it!
The beam is I-section cantilever, tapers in depth along its length (See picture attached) with a point load at the free end. I am trying to figure out the deflection formula and how to derive it! Also, when calculating its bending stress and shear stress, is it the same way as a normal beam?
Please guys, any help is appreciated it as I am completely lost!