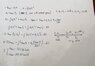Calculating Distance and Time for One-Dimensional Motion in Physics

In summary: Yes i have calculated all the quantities you mentioned, and find each distance x1,x2,x3 which add up 60km. So i think this should be correct. Thank you very much for your help!
  • #1
hquang001
31
3
Homework Statement
A train which connects city A to C, leaves the station A at 10:06 AM. The train accelerates for 6 minutes with a constant rate before it reaches its top speed. Then it is travelling with constant speed. Then it reduces its speed with a constant rate of 600 km/h² before it reaches the station of city C (The value of the speed is 0km/h when it reaches the station C). The train should arrive at city C at 10:42 AM. The distance between A to C is 60km

a) What is the acceleration of the train in the beginning ?
b) What is the maximum speed of the train ?
Relevant Equations
X = Xo + Vot + 1/2 at²
V = Vo + at
V² - Vo² = 2aX
total time: t = 36 mins = 0.6h = t1 + t2
=> t2 = t - t1 = 0.6h - 0.1h = 0.5h

Vmax = a1 x t1
Vat C = Vmax + a2t2
substitute Vmax in Vat C we have : 0 = a1 x 0.1h + (-600 km/h²) x 0.5h => a1 = 3000km/h²
Vmax = a1 x t1 = 3000 x 0.1 = 300km/h

I check the result by:
x1 = ½ a1 t1² = ½ . (3000). (0.1²) = 15km
x = ½ a2t2² + vmaxt2 + x1 = ½ (-600).(0.5²) + (300).(0.5) + 15km = 90km

I don't know why the total distance when i check the result turn out to be 90km, while the questions states that AC is 60km
 
Physics news on Phys.org
  • #2
hquang001 said:
(-600 km/h²) x 0.5h
It is not slowing down for half an hour. It spends some unstated time at constant speed.
 
  • #3
@hquang001 If I were you, I'd draw a speed vs time graph, where the distance is the area under the graph. It's easy to get lost if you only use the SUVAT equations.
 
  • #4
haruspex said:
It is not slowing down for half an hour. It spends some unstated time at constant speed.
This is the hint which i forgot to put in the question statement: It could be that you get more than one answer .

After considering your help and calculating again, i really got two possible maximum speed value like the hint stated 154751291_758301718455564_3019073286399381927_n.jpg
I want to ask how i can check if my results are correct in situation like this, or in general, one dimensional motion ?
Thank you for your help!
 
Last edited:
  • #5
PeroK said:
@hquang001 If I were you, I'd draw a speed vs time graph, where the distance is the area under the graph. It's easy to get lost if you only use the SUVAT equations.
I have done it again and also include a simple graph

hquang001 said:
This is the hint which i forgot to put in the question statement: It could be that you get more than one answer .

After considering your help and calculating again, i really got two possible maximum speed value like the hint stated View attachment 278640
 
  • #6
Have you checked your solutions? Do they both work out?
 
  • #7
PeroK said:
Have you checked your solutions? Do they both work out?
Only one solution is possible
When i substitute V = 522.09 km/h to find t3,
t3 = 0.87h which will make t2 negative
 
  • #8
hquang001 said:
Only one solution is possible
When i substitute V = 522.09 km/h to find t3,
t3 = 0.87h which will make t2 negative
Okay, so you have one good solution?
 
  • #9
PeroK said:
Okay, so you have one good solution?
Yes, Vmax = 137.91 is possible
but i don't know if it's correct or not, i don't know how to check it
 
  • #10
hquang001 said:
Yes, Vmax = 137.91 is possible
but i don't know if it's correct or not, i don't know how to check it
You have to calculate the other quantities: initial acceleration; ##t_3##, ##t_2## and check you get the right time and distance for the journey. Tricky question!
 
  • #11
PeroK said:
You have to calculate the other quantities: initial acceleration; ##t_3##, ##t_2## and check you get the right time and distance for the journey. Tricky question!
Yes i have calculated all the quantities you mentioned, and find each distance x1,x2,x3 which add up 60km. So i think this should be correct. Thank you very much for your help
 
  • Like
Likes PeroK

FAQ: Calculating Distance and Time for One-Dimensional Motion in Physics

What is motion in one dimension?

Motion in one dimension refers to the movement of an object along a single straight line or axis. This means that the object is only able to move forward or backward, left or right, or up or down in a straight line.

What is the difference between speed and velocity?

Speed is a measure of how fast an object is moving, while velocity is a measure of how fast an object is moving in a specific direction. Speed is a scalar quantity, meaning it only has magnitude, while velocity is a vector quantity, meaning it has both magnitude and direction.

How is acceleration related to motion in one dimension?

Acceleration is the rate at which an object's velocity changes over time. In one dimension, acceleration can either be positive (speeding up) or negative (slowing down). It is also directly related to the force acting on the object, according to Newton's second law of motion.

What is the difference between distance and displacement?

Distance is the total length traveled by an object, while displacement is the shortest distance between the starting and ending positions of an object. Distance is a scalar quantity, while displacement is a vector quantity.

What is the equation for calculating average speed?

The equation for average speed is: speed = distance / time. This means that to find the average speed of an object, you divide the total distance traveled by the total time it took to travel that distance.

Similar threads

Finding Maximum Velocity in Train Motion
Replies
5
Views
2K
1D Angular Motion with different velocity stages
Replies
3
Views
2K
Calculating Distance and Time for Two Cars on a One-Dimensional Road
Replies
6
Views
2K
Calculating Distance and Displacement in One Dimension
Replies
4
Views
4K
I Some thoughts about Bell's string paradox alternatives
3
Replies
75
Views
5K
Python Using Python to calculate projectile motion with resistance
Replies
2
Views
16K

Hot Threads

Recent Insights

Back
Top