Daniel_C
- 5
- 1
- Homework Statement
- Calculate the divergent amplitude of this diagram in phi-4 theory.
- Relevant Equations
- Feynman rules in momentum space for phi-4 theory.
For the diagram
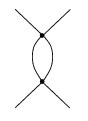
In scalar field theory, I have obtained an integral which looks like
$$\int_{0}^{\Lambda} \frac{d^4 q}{(2\pi)^4} \frac{i}{q^2 - m^2 + i\varepsilon} \frac{i}{(p - q)^2 - m^2 + i\varepsilon}$$
I am required to calculate this and obtain the divergent amplitude
$$i\mathcal{M} = ia\lambda^2[\ln{\Lambda^2} - \ln{(p_1 + p_2)^2} ]$$
The terms like $\lambda^2$ come from outside the integral, they arise due to the vertices in the diagram. I'm only really interested in how to actually go through and do this integral.
The integral is divergent in the $\ln{\Lambda^2}$ term, but we are going to tackle renormalization soon.
I'd appreciate it if someone could provide working out for the integral so that I have an example for future integrals to come.
In scalar field theory, I have obtained an integral which looks like
$$\int_{0}^{\Lambda} \frac{d^4 q}{(2\pi)^4} \frac{i}{q^2 - m^2 + i\varepsilon} \frac{i}{(p - q)^2 - m^2 + i\varepsilon}$$
I am required to calculate this and obtain the divergent amplitude
$$i\mathcal{M} = ia\lambda^2[\ln{\Lambda^2} - \ln{(p_1 + p_2)^2} ]$$
The terms like $\lambda^2$ come from outside the integral, they arise due to the vertices in the diagram. I'm only really interested in how to actually go through and do this integral.
The integral is divergent in the $\ln{\Lambda^2}$ term, but we are going to tackle renormalization soon.
I'd appreciate it if someone could provide working out for the integral so that I have an example for future integrals to come.