Calculating F, V and C: Why Can It Not Be Obtained This Way?

[hidemi]

Homework Statement

A 0.20-kg particle moves along the x axis under the influence of a conservative force. The potential energy is given by

U(x) = (8.0 J/m^2)x^2 + (2.0 J/m^4)x^4,

where x is in coordinate of the particle. If the particle has a speed of 5.0 m/s when it is at x = 1.0 m, its speed when it is at the origin is:

a) 0 m/s
b) 2.5 m/s
c) 5.7 m/s
d) 7.9 m/s
e) 11 m/s

The answer is E.

Relevant Equations

K1 + U1 = K2 + U2

The correct answer can be obtained by the calculation as attached.

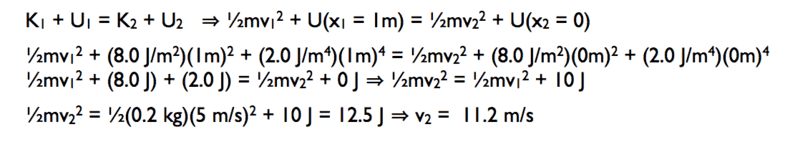
However it can not be gotten by the following way. Why?
F = -∇U = -[ 16x + 8x^3] = ma
Since m = 0.2, a = -80x - 40x^3
V = -40x^2 - 10x^4 +C =5
c= 50 + 5 =55

 

[Orodruin]

You have treated acceleration as if it were the derivative of velocity with respect to position when it is the derivative of velocity with respect to time.

 

[Delta2]

Your mistake is that the velocity is the integral of acceleration with respect to time t , not with respect to the distance or x-coordinate. So your line

V=-40x^2-10x^4+C

is wrong. To continue with your way, you should set $a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=\frac{dv}{dx}v$ and solve the ODE $$-16x-8x^3=m\frac{dv}{dx}v$$ by the separating variables technique.

 

[hidemi]

Your mistake is that the velocity is the integral of acceleration with respect to time t , not with respect to the distance or x-coordinate. So your lineis wrong. To continue with your way, you should set $a=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=\frac{dv}{dx}v$ and solve the ODE $$-16x-8x^3=m\frac{dv}{dx}v$$ by the separating variables technique.

Thanks for your remider :)

 

[Orodruin]

Similar technique, but slightly different on execution is to let a dot denote derivative with respect to time, i.e., $a = \ddot x$ and $v = \dot x$. The equation of motion becomes
$$
\ddot x = -80x - 40 x^3.
$$
Multiplying both sides with $v = \dot x$ leads to
$$
v \dot v = \ddot x \dot x = -80 x \dot x - 40 x^3 \dot x.
$$
Noting that for any function $g(t)$, it holds that $d(g^n)/dt = n g^{n-1} \dot g$ therefore leads to
$$
\frac{d}{dt} \left[\frac 12 v^2\right] = \frac{d}{dt}\left[ - 40 x^2 - 10 x^4\right],
$$
which means the expressions being differentiated differ by a constant, which is essentially the conservation of energy equation.