Calculating Heat Flow Through a Rod: Step-by-Step Guide

Click For Summary
SUMMARY

This discussion focuses on calculating the rate of heat flow through a rod in a steady state using the formula ΔQ/Δt = [KA($2 - $1)] / x, where K is thermal conductivity, A is the cross-sectional area, and x is the thickness. The participants emphasize the need for integration due to the varying cross-sectional area and clarify that the correct relationship is $2 > $1. The final equation presented is H = -kA(dT/dx), which simplifies to H = -kπr²(dT/dx), highlighting the importance of understanding the relationship between the radius (r) and the position (x) for accurate integration.

PREREQUISITES
  • Understanding of heat transfer principles
  • Familiarity with thermal conductivity concepts
  • Basic knowledge of calculus, specifically integration
  • Ability to manipulate algebraic equations
NEXT STEPS
  • Study the derivation of the heat conduction equation in cylindrical coordinates
  • Learn about the concept of steady-state heat transfer
  • Explore integration techniques for variable cross-sectional areas
  • Investigate practical applications of heat flow calculations in engineering
USEFUL FOR

Students and professionals in thermal engineering, mechanical engineering, and physics who are involved in heat transfer analysis and require a solid understanding of the principles governing heat flow through materials.

Wiz
Messages
21
Reaction score
0
Hi,
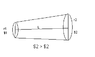
I have to find the rate of heat flow through a cross-section of the rod in steady state as shown in the figure.Thermal conductivity of the rod is K.
I have used a $(dollar) sign for theta.
The formula i know is ΔQ/Δt = [KA($2 - $1)] /x
where ΔQ/Δt is the heat current,where A is area of cross section and x is the thickness.
since the area of cross section varies.i think integration will be used...
can ANYBODY GUIDE ME THROUGH..??
[NOTE - THE FIGURE READ THAT $2 > $2 , which is a mistake and the correction is $2 > $1.]
Thanks,
 

Attachments

  • heat conduction.gif
    heat conduction.gif
    1.1 KB · Views: 605
Physics news on Phys.org
1. assume that the steady state
2. get a thin slice of tube
3. since steady state: heat enter=heat exit
4. this means H is constant over all x
5. our equation:
H=-kA(dT/dx)​
H=-k*pi*r^2*(dT/dx)​
7. well, pi is constant over all x
8. well, r is not constant over all x
9. good luck integrating...
 
??

how do i relate x and r...
there are 3 variables and we need only 2 for integration.
hope u understand,
wiz

(btw - all the steps u wrote were know to me already0
 

Similar threads

How Does Thermal Conductivity Affect Heat Transfer Between Two Water Vessels?
  • · Replies 1 ·
Replies
1
Views
1K
Two rods are connected one silver and the other gold.
  • · Replies 3 ·
Replies
3
Views
7K
Heat flow through aluminium rod
  • · Replies 6 ·
Replies
6
Views
2K
How Does Heat Transfer Through Different Metals?
  • · Replies 2 ·
Replies
2
Views
4K
Heat flow problem (copper pipe)
  • · Replies 2 ·
Replies
2
Views
2K
What is the Work Done by a Heated Metal Rod?
  • · Replies 2 ·
Replies
2
Views
3K
Heat flux through a material with variable heat conductance
  • · Replies 2 ·
Replies
2
Views
2K
Heat transfer through a cylindrical shell
  • · Replies 3 ·
Replies
3
Views
3K
Behavior of heat addition in a compressible flow
  • · Replies 9 ·
Replies
9
Views
4K
Heat Flow in Three Identical Rods of Metal
  • · Replies 3 ·
Replies
3
Views
3K