koomba
- 9
- 0
Ok I've been working on this problem for a while, and I'm kinda new to physics, so bear with me. So here it is:
Heres the picture of the problem:
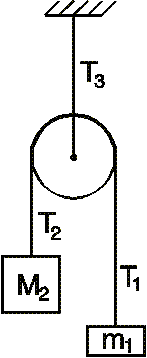
A frictionless pulley with zero mass is attached to the ceiling, in a gravity field of 9.81 m/s2. Mass M2=0.150 kg is being accelerated downward with a=1.10 m/s2. Calculate the mass m1.
Just assume there is no compression/stretching of the rope on this problem. ALso, I guess the acceleration of M1 would be -1.10 m/s^2, correct? Beyond this I'm really confused. Any help would be greatly appreciated! Thanks.
Steven
Heres the picture of the problem:
A frictionless pulley with zero mass is attached to the ceiling, in a gravity field of 9.81 m/s2. Mass M2=0.150 kg is being accelerated downward with a=1.10 m/s2. Calculate the mass m1.
Just assume there is no compression/stretching of the rope on this problem. ALso, I guess the acceleration of M1 would be -1.10 m/s^2, correct? Beyond this I'm really confused. Any help would be greatly appreciated! Thanks.
Steven