Calculating Moment: Addition of Torque Components

[Saptarshi Sarkar]

Homework Statement

In order to pull out the nail at B, as shown in the figure, the force F exerted on the handle of the hammer must produce a clockwise moment of 500 lb-in about point A. Determine the required magnitude of force F.

Relevant Equations

$T=F\times l$

First of all, sorry for the units. This is a problem I found on the internet and am confused about the solution.

I calculated the two components of the moment (torque) to be

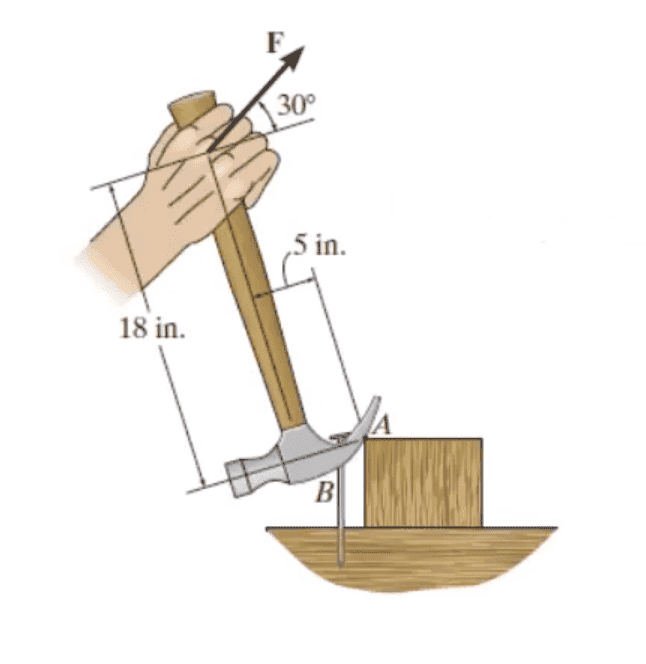
$T_x = 18\times Fcos(30)$ and $T_y=5\times Fsin(30)$

The problem is, I got the proper answer (the two options were 27.64 lb and 55.28 lb) by direct addition of the two components but did not get it by vector addition (for magnitude).

I am not sure how I got the correct answer using a seemingly incorrect method.

 

[haruspex]

The torque vector is the cross product of the force vector and the lever arm vector. So what direction is it in?

 

[Lnewqban]

Solution #1 is correct because both components of F (x and y) are perpendicular to the lever of each respect to the point A, where the moment said to be applied.
Solution #2 is incorrect because you are mixing torque with your effort to determine F from its x and y components.

 

[Saptarshi Sarkar]

The torque vector is the cross product of the force vector and the lever arm vector. So what direction is it in?

Got it. Both of the them are pointing in the same direction, so it should be added normally. Thanks!