Calculating Net Force of Particle 5: A Problem Overview

[Fontseeker]

I have the following problem:

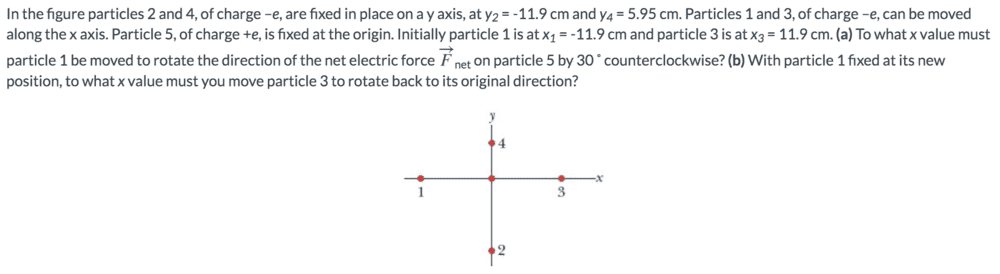
So, I know the following:
$q_1 = -e$
$q_2 = -e$
$q_4 = -e$
$q_5 = e$
$e = 1.6*10^{-19}$
$k = 9*10^{9}$

Now, I can get the current $F_{net}$ of particle 5 with this information:

$F_{net} = (F_{3} - F_{1})\hat i + (F_{2} + F_{4})\hat j$
$F_{1} = k * \frac{e * e}{x_1^2} = 1.627 * 10^{-26}N$
$F_{2} = k * \frac{e * e}{y_2^2} = 6.508 * 10^{-26}N$
$F_{3} = k * \frac{e * e}{x_3^2} = 1.627 * 10^{-26}N$
$F_{4} = k * \frac{e * e}{y_4^2} = 1.627 * 10^{-26}N$

Now, I can break up $F_{net}$ into components:
$F_{x} = (1.627 * 10^{-26} - 1.627 * 10^{-26})N =0N$
$F_{y} = (6.508 * 10^{-26} - 1.627 * 10^{-26})N = 4.881 * 10^{-26}N$

To rotate $F_{net}$ by 30 degrees, I know the y component will not change, so I can make this assumption:
$\tan \theta= \frac{F_x}{F_{y}}$
so
${F_x} = \tan \theta * F_{y} = \tan 30 * 4.881 * 10^{-26}N = 2.818 * 10^{-26}N$
and since it is rotating counterclockwise, the x component must be negative:
${F_x} = -2.818 * 10^{-26}N$
Now, to find the new position, r, of particle 1 to get this new ${F_x}$ for the net charge of particle 5
${F_x} = {F_3} - {F_1}$
${F_1} = {F_3} - {F_x}$
${F_1} = {F_3} - {F_x}$
$k * \frac{e * e}{r^2} = {F_3} - {F_x}$
$r = \sqrt {\frac{k * e * e}{{F_3} - {F_x}}}$
$r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} - (-2.818 * 10^{-26})}}$
$r = \sqrt {\frac{k * e * e}{1.627 * 10^{-26} + 2.818 * 10^{-26}}}$
$r = 0.071995m$

So, the new position of particle 1 is at (0.071995m, 0), which is my answer for part A. Now, for part B, the new position of particle 3 would have to be (-0.071995m, 0). However, this is the wrong answer. Does anyone see my mistake?

 

[Delta2]

I believe by rotation it means rotation without changing the magnitude of the vector. In your calculations the magnitude of $F_{net}$ does not remain constant as it rotates. I believe the core of your mistake lies in this line

To rotate FnetFnetF_{net} by 30 degrees, I know the y component will not change, so I can make this assumption

I think the y component must also change so that the new $F_x$ and the new $F_y$ result in a vector that has the same magnitude as before.

 

[Fontseeker]

I believe by rotation it means rotation without changing the magnitude of the vector. In your calculations the magnitude of $F_{net}$ does not remain constant as it rotates. I believe the core of your mistake lies in this line

I think the y component must also change so that the new $F_x$ and the new $F_y$ result in a vector that has the same magnitude as before.

If the y component will also change, then I would have several unknowns. I wouldn't know the position of particle 1, particle 4, and particle 2.

 

[Delta2]

Hm yes you are right, upon closer examination of the statement, it just states "to rotate the direction" and not to "rotate the vector"
Hold on while i check the rest of your work.

 

[Delta2]

Hi, sorry for the late response, i really had to leave.

The only mistake I see is at the sign of the position of particle 1, it must be at $x=-0.071995$ while the new position of particle 3 at $x=0.071995$ if we take the x-axis to be positive at the right. You lost information about the sign because you took the positive square root, while there is the negative square root also that is $-\sqrt {K\frac{ee}{F_3-F_x}}$ which is also a valid solution to the equation. We have to choose the negative solution because only then the force from particle 1 to particle 5 is towards to the left and since we want the total force on x-axis to be towards to the left.

Another mistake i see that does not affect your end results is that since if we look at the statement for the $y_2$ and $y_4$ it should be
$F_2=1.627\times 10^{-26}$ and $F_4=6.508\times 10^{-26}$
Also since it seems that by $F_n$ $n=1,2,3,4$ you denote the magnitude of the force, the equation about $F_{net}$ should be
$\vec{F_{net}}=(F_3-F_1)\hat i+(F_4-F_2)\hat j$
However you denote as $F_x$ not only the magnitude but the direction since you give it a negative value , so you actually mixing things up denoting by $F_n$ the magnitude and by $F_x$ magnitude and direction. It should be better if you stated $\vec{F_x}=-2.818\times 10^{-26}\hat i$. But then again this doesn't affect your end result.

 

[Fontseeker]

Hi, sorry for the late response, i really had to leave.

The only mistake I see is at the sign of the position of particle 1, it must be at $x=-0.071995$ while the new position of particle 3 at $x=0.071995$ if we take the x-axis to be positive at the right. You lost information about the sign because you took the positive square root, while there is the negative square root also that is $-\sqrt {K\frac{ee}{F_3-F_x}}$ which is also a valid solution to the equation. We have to choose the negative solution because only then the force from particle 1 to particle 5 is towards to the left and since we want the total force on x-axis to be towards to the left.

Another mistake i see that does not affect your end results is that since if we look at the statement for the $y_2$ and $y_4$ it should be
$F_2=1.627\times 10^{-26}$ and $F_4=6.508\times 10^{-26}$
Also since it seems that by $F_n$ $n=1,2,3,4$ you denote the magnitude of the force, the equation about $F_{net}$ should be
$\vec{F_{net}}=(F_3-F_1)\hat i+(F_4-F_2)\hat j$
However you denote as $F_x$ not only the magnitude but the direction since you give it a negative value , so you actually mixing things up denoting by $F_n$ the magnitude and by $F_x$ magnitude and direction. It should be better if you stated $\vec{F_x}=-2.818\times 10^{-26}\hat i$. But then again this doesn't affect your end result.

thanks

 

[Delta2]

thanks

What does your textbook answer key says, is x=-0.071995 the correct answer (for particle 1)?

 

[Fontseeker]

What does your textbook answer key says, is x=-0.071995 the correct answer (for particle 1)?

yes