Chijioke
- 14
- 3
Misplaced Homework Thread
The water level in a spherical bowl has a diameter of 30 cm. If the horizontal diameter of the bowl is 10 cm below the water level, calculate the radius of the bowl and the depth of the water in the bowl.
I managed to draw a diagram below:
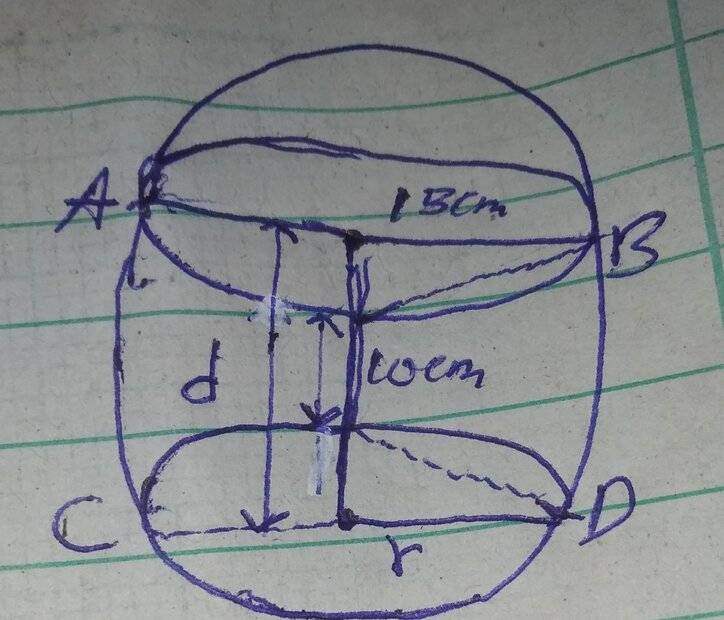
In my drawing, I am seeing the sphere ABCD as the spherical bowl and the AB as the diameter of the water level.
I also see CD as the horizontal diameter of bowl which is below the water level and d as depth of the water.
If think I am having problem interpreting the problem based on what I have drawn.
I managed to draw a diagram below:
In my drawing, I am seeing the sphere ABCD as the spherical bowl and the AB as the diameter of the water level.
I also see CD as the horizontal diameter of bowl which is below the water level and d as depth of the water.
If think I am having problem interpreting the problem based on what I have drawn.