- #1
nixed
- 35
- 0
In considering the shortest paths between two points on a sphere I came across the following interesting problem:
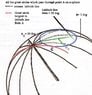
An ant sits on the outside of a glass bowl of spherical curvature (radius R), at a distance d from the lip of the bowl. It sees a drop of honey on the inside of the bowl directly opposite it (i.e. also a distance d from the lip and 180° round the bowl from the ant. What is the shortest path for the ant to take to get the honey? Is it unique?
I know that the shortest distance between two points on the surface of a sphere is along a great circle which passes through the two points and is centered at the sphere origin O.
There are three distinct cases which depend on the depth of the bowl (i.e. the vertical distance from rim to base).
case 1. depth < R
case 2. depth = R
case 3. depth > R
What are the shortest paths for each of these cases and how do they differ from each other?
An ant sits on the outside of a glass bowl of spherical curvature (radius R), at a distance d from the lip of the bowl. It sees a drop of honey on the inside of the bowl directly opposite it (i.e. also a distance d from the lip and 180° round the bowl from the ant. What is the shortest path for the ant to take to get the honey? Is it unique?
I know that the shortest distance between two points on the surface of a sphere is along a great circle which passes through the two points and is centered at the sphere origin O.
There are three distinct cases which depend on the depth of the bowl (i.e. the vertical distance from rim to base).
case 1. depth < R
case 2. depth = R
case 3. depth > R
What are the shortest paths for each of these cases and how do they differ from each other?